Источник направленного света

Более эффективной (в смысле количества вычислений) альтернативой точечному источнику света является источник направленного света (directional light). Источник направленного света имеет ориентацию, но не имеет заданного расположения. Лучи, излучаемые источником направленного света, параллельны друг другу. При создании сцен с использованием направленного света будет казаться, что источник света находится очень далеко от объектов сцены.

Источник зонального света

Источник зонального света, или прожектор, (spot light) имеет ориентацию и заданное местоположение, и излучает световой поток в форме конуса. Характеристики конуса определяются углами светового пятна (hotspot или umbra) и зоны освещенности (fallof или penumbra). Угол светового пятна определяет конус, в котором интенсивность зонального света максимальна. Угол зоны освещенности определяет конус света с уменьшающейся интенсивностью вокруг светового пятна. Угол зоны освещенности источника зонального освещения всегда больше угла светового пятна.

Direct3D поддерживает источники рассеянного света, точечные и направленные источники света, а также источники зонального света. Также Direct3D предлагает вариант направленного источника света, называемый параллельным источником света (parallel light).

Каркасный метод

Каркасный метод визуализации (wireframe rendering) не предназначен для создания реалистичных изображений и не требует выполнения всех тех действий, которые мы обсуждали до этого. В каркасных моделях выводятся только края граней объектов сцены, изображаемые прямыми линиями. На рис.2.22 изображена сетка, выведенная в каркасном режиме.

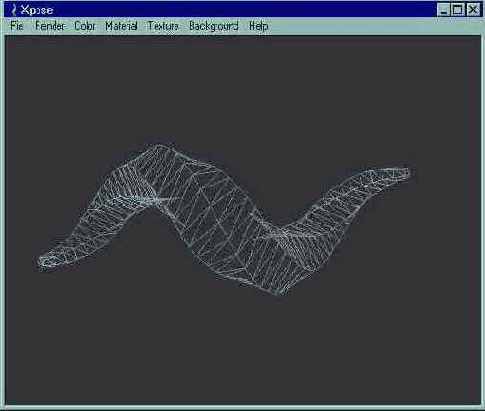
Рис. 2.22. Каркасный метод визуализации

Ключевые кадры

Термин ключевые кадры (key-framing) пришел из традиционной техники анимации, где определяются только несколько «ключевых» кадров. Оставшиеся кадры создаются как промежуточные позиции между ключевыми.

Метод ключевых кадров в трехмерной анимации означает, что вы определяете позиции объектов сцены в ключевые моменты анимации. Компьютер берет на себя задачу размещения объектов на промежуточных кадрах.

Метод ключевых кадров требует, чтобы вы определили количество кадров в анимационной последовательности и задали ключи для определенных кадров. Например, если вам требуется создать анимацию, в которой объект перемещается из верхнего левого угла экрана в верхний правый угол, а затем в нижний правый, вам необходимо выполнить следующие шаги:

В Direct3D имеются два режима для метода ключевых кадров: линейный (linear) и сплайновый (spline-based). В линейном режиме движение между ключевыми кадрами осуществляется линейно, объект перемещается по кратчайшему пути. При сплайновой анимации для перемещения между ключевыми кадрами используются изогнутые траектории.

В нашем примере в случае линейной анимации объект будет перемещаться по прямой из верхнего левого угла экрана в верхний правый. В кадре 15 (когда объект находится в верхнем правом углу) объект резко развернется и направится в нижний правый угол. В сплайновой анимации объект будет срезать угол по дуге. Объект будет вести себя так, как будто он предвидит, что впереди его ждет поворот.

И в линейной и в сплайновой анимации в ключевых кадрах объект будет находиться точно в указанном месте сцены.

Масштабирование

Выполнение операции масштабирования над сеткой или гранью изменяет ее размер и местоположение. Сначала давайте посмотрим, как с помощью операции масштабирования можно изменить размеры объекта. Если мы возьмем наш куб, размерами 1x1x1 и произведем операцию масштабирования с коэффициентом 1/2, длина каждой грани нашего куба станет равна 1/2 (получим куб размером 1/2x1/2x1/2). Если же мы используем коэффициент масштабирования, равный 2, то мы удвоим размеры нашего куба, получив куб с размером каждой грани 2единицы (то есть куб размерами 2x2x2). На рис. 2.13. показаны результаты рассмотренных операций масштабирования.

Рис. 2.13. Результаты масштабирования куба размерами 1x1x1 с коэффициентами 1/2 и 2

Как упоминалось ранее, операция масштабирования также изменяет местоположение объекта. На рис. 2.13 центр куба совпадает с началом координат. Если бы этого не было, то операция масштабирования повлияла и на местоположение куба и на его размер. Операция масштабирования не увеличивает непосредственно объект: она проводится над вершинами объекта. Когда коэффициент масштабирования больше 1, вершины удаляются от начала координат. Когда коэффициент масштабирования меньше 1, вершины приближаются к началу координат. На рис. 2.14 показан результат операции масштабирования с теми же коэффициентами, что и на рис. 2.13, но исходный куб был сдвинут вправо по оси Y и куб, полученный в результате операции масштабирования, располагается дальше от начала координат.

Рис. 2.14. Перемещение и изменение размеров куба в результате операции масштабирования

Часто этот эффект нежелателен, если нам необходимо масштабировать объект без изменения его местоположения. В этом случае мы перемешаем объект в начало координат, масштабируем его и возвращаем на прежнее место. Некоторые графические системы (включая Direct3D) допускают операции масштабирования, которые изменяют размеры объекта без изменения его местоположения, независимо от того, совпадает ли центр объекта с началом координат. Эта операция выполняется путем использования локальных, или объектных, осей координат. Масштабирование объекта с использованием локальных осей производит тот же эффект, что и масштабирование объекта, центр которого совпадает с началом координат: размеры объекта изменяются, а его местоположение (координаты центра объекта) остается неизменным. По умолчанию Direct3D при операции масштабирования использует локальные оси координат объекта.

Мы можем задавать различные коэффициенты масштабирования для каждой из осей. Это позволяет растягивать и сжимать объекты. Коэффициент масштабирования, равный 1, не оказывает влияния на вершины объекта, таким образом, коэффициент 1 может использоваться для оси, вдоль которой размер объекта не должен изменяться. Если мы выполним с нашим исходным кубом операцию масштабирования с коэффициентами <2, 1, 1>, то мы в два раза увеличим ширину куба, не меняя остальных его размеров. Результат этой операции можно увидеть на рис. 2.15.

Рис. 2.15. Результат операции масштабирования с коэффициентами <2, 1, 1>

Масштабирование текстуры

Текстуры могут накладываться на объект несколькими различными способами. Один из способов изменения текстуры называется масштабированием текстур. Если текстура накладывается с увеличивающим размер коэффициентом масштабирования, то на объекте будет видна только ее часть. Если коэффициент масштабирования уменьшает размер текстуры, то на объекте текстура будет повторена несколько раз. Последний эффект может быть весьма полезен, когда вам необходимо представить большой объект, рисунок поверхности которого представляет собой набор повторяющихся фрагментов. На рис. 2.18. изображена одна и та же текстура с разными коэффициентами масштабирования.

Рис. 2.18. Пример масштабирования текстуры

Метод Фонга

Закраска по методу Фонга (Phong shading) является усовершенствованием метода Гуро. Подобно методу Гуро, в методе Фонга используются нормали вершин, однако, вместо интерполяции вычисленных для вершин значений, производится вычисление нормалей для каждой точки грани. Эта дополнительная работа обеспечивает более точный результат. Как вы можете догадаться, закраска по методу Фонга медленнее, чем закраска по методу Гуро. Иллюстрация для этого метода не приводится, поскольку на момент написания книги Direct3D не поддерживал закраску по методу Фонга.

Метод Гуро

Закраска методом Гуро (Gouraud shading) подобна равномерной закраске, за исключением того, что нормали рассчитываются для каждой вершины вместо того, чтобы рассчитывать их для каждой грани. Грань закрашивается с использованием интерполяции значений освещенности в вершинах. Это приводит к сглаживанию изображения сеток, и отдельные грани становятся неразличимыми. Закраска методом Гуро позволяет получить реалистичные изображения, но может сделать объекты неотчетливыми и смутными. Поскольку используются нормали к вершинам и усредненные значения для грани, метод Гуро требует большего объема вычислений, чем равномерная закраска. Закраска по методу Гуро использовалась для рис. 2.25.

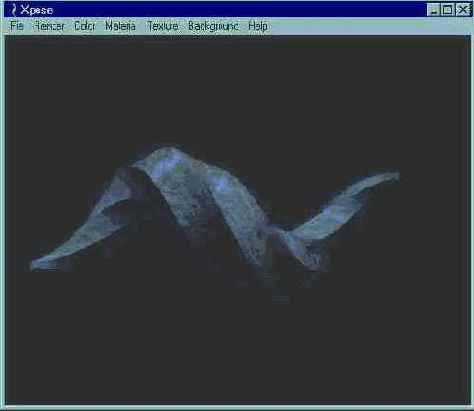
Рис. 2.25. Закраска по методу Гуро

Методы визуализации

Как только сцена была смоделирована в трех измерениях и преобразована в двухмерный вид, она готова к визуализации. Этот заключительный шаг создания изображения, которое будет выведено на ваш экран, называется визуализацией или рендерингом (rendering или shading). Существует несколько различных методов визуализации, и сейчас мы коротко рассмотрим наиболее часто применяемые.

Начало системы координат

Точка, в которой пересекаются все три координатных оси, называется началом системы координат (origin). Для этой точки координаты X, Y и Z равны нулю: <0, 0, 0>. Чем больше координата точки отличается от нуля, тем дальше точка от начала координат. У точек расположенных справа от начала координат значение X положительное, у точек, расположенных слева — отрицательное. Подобным образом, точки расположенные выше начала координат характеризуются положительным значением Y, а точки расположенные ниже — отрицательным. На рис. 2.2 показаны несколько точек с их координатами.

Рис. 2.2. Точки с соответствующими координатами

На рисунке точки представлены как сферы. Это сделано для того, чтобы их можно было увидеть, поскольку точки определяют местоположение, но не являются объектами. На рис. 2.3 показаны несколько точек, которые расположены в разных местах вдоль оси Z.

Рис. 2.3. Точки вдоль оси Z

Наложение текстур

Наложению текстур стали уделять большое внимание после выхода программы DOOM, выпущенной ID Software. Конечно, DOOM не первая программа, в которой применялось наложение текстур, но эта программа стала наиболее популярной.

Наложение текстур (texture mapping) определяет способ, которым при получении изображения текстура соединяется с гранью или набором граней. Наложение зависит от положения объекта в пространстве. Мы не можем просто налепить текстуру на поверхность, не учитывая расстояние до объекта и его ориентацию относительно зрителя. Такая сцена будет плохо выглядеть. Дальше в этой главе мы поговорим подробнее о текстурах и перспективе. А пока запомните, что способ наложения текстур на удаленные объекты, должен отличаться от способа наложения текстур на объекты, расположенные ближе к зрителю.

Неосвещенный метод

Неосвещенный метод визуализации (unlit rendering) получил свое название из-за того, что при его применении наличие источников света игнорируется. Грани рисуются с использованием назначенных им цветов и текстур без учета значений освещенности или ориентации грани. Сцены с применением неосвещенного метода создаются быстро, но объекты в этих сценах оказываются похожими на силуэты. Рис. 2.23 показывает результат использования данного метода визуализации.

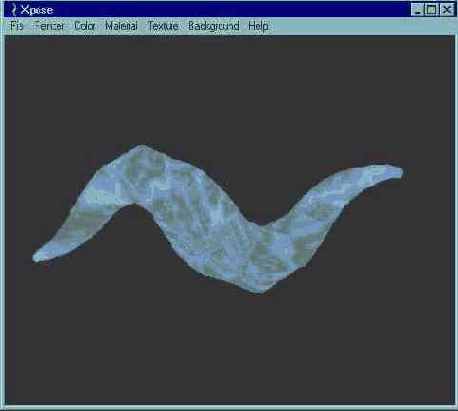
Рис. 2.23. Неосвещенный метод визуализации

Нормали

Нормали (normals) представляют собой векторы, используемые при вычислении цветов для граней и сеток. Существует два типа нормалей: нормали к грани и нормали к вершине.

Нормаль к грани — это вектор, перпендикулярный этой грани. Нормаль определяет цвет грани и то, какая из сторон грани видимая. На рис. 2.9 изображен куб со стрелками, представляющими нормали к граням.

Рис. 2.9. Нормали к граням куба

Нормали к вершине — это векторы, которые присваиваются каждой вершине в сетке. Ориентация каждого вектора зависит от ориентации и размера соединяющихся в вершине граней. Рис. 2.10 показывает нормали к вершинам куба.

Рис. 2.10. Нормали к вершинам куба

Использование нормалей к граням или нормалей к вершинам определяется методом визуализации. Некоторые методы визуализации используют нормали к граням, другие — нормали к вершинам, а некоторые методы не используют нормали вообще. Позже в этой главе мы поговорим о методах визуализации.

В большинстве случаев, Direct3D вычисляет и использует нормали автоматически, так что нет необходимости, чтобы вы знали об их существовании. Однако имеются ситуации, когда нормали могут быть переопределены для получения специальных эффектов. Подробнее мы поговорим о нормалях в главе 8.

Освещение

Наши перемещаемые, масштабируемые, вращаемые и текстурированые объекты могут существовать в трехмерном пространстве и никогда не будут замечены, если останутся в темноте. Прежде чем мы сможем что-нибудь увидеть, необходимо обеспечить источник света. Когда мы увидим окончательный результат, все объекты сцены будут представлены в соответствии с параметрами установленных в сцене источников света.

От трех измерений к двум

Переход от трех измерений к двум требует, разделения трехмерного пространства на части, таким образом, чтобы двухмерное изображение могло быть легко получено. Это значит, что нам необходимо определить, где будет располагаться зритель, или камера, и какую часть сцены он должен видеть. Все эти параметры определяют область видимого пространства (viewing frustum). Мы будем представлять область видимого пространства как пирамиду. Зритель располагается в вершине пирамиды и смотрит в центр ее основания. Если увеличить основание пирамиды, будет видна большая часть сцены, но сами объекты станут более мелкими. Если размер основания уменьшить, объекты будут казаться более крупными, но при этом зритель увидит меньшую часть сцены. Размер основания пирамиды определяется углом зрения или параметрами поля зрения (FOV).

На рис. 2.21 изображена одна и та же сцена с различных углов. На левом рисунке мы видим пирамиду, изображающую область видимого пространства. Стрелка указывает направление взгляда зрителя. На рисунке справа приведено изображение, которое является результатом использования данных параметров области видимого пространства.

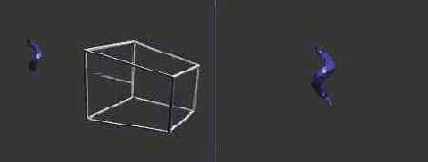
Рис. 2.21. Область видимого пространства и полученное изображение

Использование различных параметров области видимого пространства подобно замене линз объектива вашей камеры. Используя телеобъектив, вы сможете видеть удаленные объекты, но не сможете сделать семейную фотографию, пока не отойдете на 400 футов. С другой стороны, вы можете использовать широкоугольный объектив для съемки крупным планом, но такой объектив не подойдет для наблюдения за птицами (если птица, за которой вы наблюдаете, не находится в клетке).

Параметры движения

Один из простейших способов анимации— задание атрибутов движения (motion attributes). Атрибуты движения — это операции перемещения, вращения и масштабирования, которые применяются к объекту или набору объектов при каждом обновлении изображения. Атрибуты движения используются для простых, повторяющихся движений. Как только объекту будут назначены атрибуты движения, он будет перемещаться в соответствии с ними без всякого дополнительного вмешательства.

Перемещение

Давайте попробуем переместить наш куб вверх от начала координат на две единицы. Мы можем выполнить это, используя перемещение <0, 2, 0>. Результат изображен на рис. 2.12.

Рис. 2.12. Куб после перемещения <0, 2, 0>

Объекты могут быть перемещены по нескольким осям одновременно с использованием одной операции, так что нет необходимости выполнять отдельные операции для сдвига объекта вдоль каждой из осей. Например, перемещение <2, 2, 0> передвинет куб на две единицы вправо и на две единицы вверх.

Перспективное преобразование

В начале этой главы я упомянул, что целью трехмерной графики является создание двухмерного представления трехмерной сцены. Мы обсудили совершение различных действий в невидимом, трехмерном пространстве; теперь настало время обсудить получение двухмерной версии трехмерного мира.

Переход от трех измерений к двум требует перспективного преобразования. Перспективное преобразование гарантирует, что полученное в результате изображение будет выглядеть и вести себя корректно. Корректное поведение подразумевает, что объекты, расположенные ближе к зрителю будут казаться больше, чем объекты, расположенные вдалеке. Это также значит, что объекты или части объектов, расположенные вне пределов видимости не будут рисоваться. Также нам необходимо решить, когда объект находится слишком близко или слишком далеко, чтобы рисовать его.

Плоскости

Плоскость (plane) это плоская поверхность, простирающаяся до бесконечности. Плоскость не является квадратом или прямоугольником, поскольку и квадрат и прямоугольник имеют грани и углы. Размер плоскости не определен. Простейший способ задать плоскость — указать ось и координату точки пересечения плоскости с этой осью. Например, плоскость, определяемая значением Y равным -3 расположена на три единицы ниже начала координат и распространяется до бесконечности вдоль осей X и Z. Эта плоскость пересекает ось Y перпендикулярно в точке с координатой -3. Часть такой плоскости показана на рис. 2.5.

Рис. 2.5. Часть плоскости пересекающей ось Y в точке -3

Заметьте, что, определяя плоскость с помощью оси и координаты, мы не можем задать плоскость, которая не была бы параллельна двум другим осям. Если мы хотим определить плоскость, которая, например, пересекает ось Y под углом 45 градусов, нам необходимо более сложное представление.

Мы можем использовать вектор, чтобы определить ориентацию плоскости. Если нам необходима плоскость, пересекающая ось Y под углом 45 градусов, мы можем использовать вектор <0, 1, -1>, чтобы определить наклон плоскости по отношению к зрителю (вектор перпендикулярен определяемой плоскости). Одного вектора недостаточно, чтобы определить плоскость, он указывает только ориентацию. Мы нуждаемся еще в указании местоположения плоскости. Можно снова использовать координату Y равную -3, чтобы указать, что плоскость пересекает ось Y на три единицы ниже начала координат. Часть этой плоскости изображена на рис. 2.6.

Рис. 2.6. Плоскость, расположенная в точке Y=-3 и ориентированная вектором <0, 1, -1>

Преобразования

Итак, мы узнали, как разместить объекты в трехмерном пространстве. Мы можем задать вершины, используя вершины определить грани, а из граней создать сетку. Теперь нам необходимо узнать способы изменять положение существующих объектов. Есть три основных операции, которые могут использоваться для изменения положения объекта в пространстве: перемещение (translate), масштабирование (scale) и вращение (rotate). Используя эти три операции, мы можем переместить объект в любое место и придать ему любую ориентацию.

Прежде чем мы продолжим, давайте создадим простую сцену, которая будет применяться при обсуждении операций перемещения, масштабирования и вращения. Мы будем использовать простую сетку— куб. Центр нашего куба будет совпадать с началом координат, а размеры всех его граней будут равны 1. Такой куб показан на рис. 2.11.

Рис. 2.11. Куб для изучения преобразований

Заметьте, что поскольку центр куба совпадает с началом координат, стороны куба отстоят от центра на 1/2 единицы в каждом направлении вдоль каждой из осей координат. Также отметим, что каждая грань (каждая сторона куба) перпендикулярна пересекающей ее оси.

Природа текстуры

Текстура представляет собой двухмерное цветное изображение. Часто текстуры хранятся в файлах типа BMP, PCX или GIF. Практически любое двухмерное изображение можно использовать как текстуру. Пример текстуры вы можете увидеть на рис.2.17.

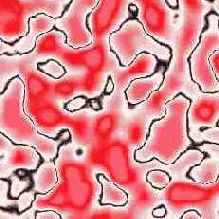
Рис. 2.17. Пример текстуры

Прежде чем вы начнете использовать различные изображения в качестве текстур, обратите внимание на одну особенность — не все изображения будут хорошими текстурами. Хорошие текстуры обычно не предназначены для отдельного просмотра, но они придают реализм объектам. Изображения, на которых представлены законченные сцены, обычно не годятся для использования в качестве текстур, поскольку вы не ожидаете увидеть законченную сцену, глядя на единственную грань объекта. Такие трехмерные объекты, как зеркала и картины, являются исключением из этого правила.

Рассеянный свет

Простейший источник света— это рассеянный свет (ambient light). Источник рассеянного света не имеет местоположения и освещает все объекты сцены с одинаковой интенсивностью. Это освещение удобно, потому что его просто использовать. Часто рассеянный свет используется в комбинации с более сложными источниками света.

Равномерная закраска

Равномерная закраска (flat shading) позволяет получить более реалистичное изображение, чем каркасный или неосвещенный методы визуализации. При равномерной закраске учитывается освещенность грани. Для каждой грани вычисляется нормаль, которая применяется для вычисления параметров освещенности всей грани. Равномерная закраска требует большего объема вычислений, чем каркасный и неосвещенный методы. Рис.2.24 показывает сцену, визуализированную с применением равномерной закраски. Обратите внимание, как выделяется каждая грань.

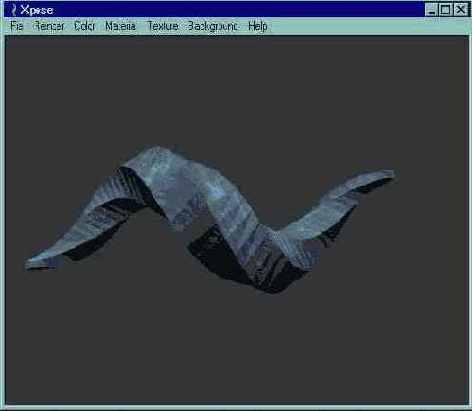
Рис. 2.24. Изображение, полученное методом равномерной закраски

Сетки

Сетка (mesh) — это набор соединенных граней. Обычно сеть описывает один объект в сцене. Сетка может объединять одну или несколько граней, и может быть очень сложной. На рис. 2.8 показан пример сетки. Если вы внимательно посмотрите на рисунок, то сможете выделить отдельные грани.

Рис. 2.8. Визуализированная сеть

Способы наложения текстуры

Способ наложения текстуры (texture wrapping) определяет, каким образом текстура будет соединяться с объектом. Простейший способ наложения предполагает, что текстура попадает на объект как выстреленная из пушки. В этом случае цвета текстуры проходят объект насквозь и появляются с другой его стороны. Такой метод обычно называется плоским наложением (небольшой парадокс, поскольку вы не можете обернуть объект, чем-то, что действительно является плоским). Рис.2.19 показывает результат плоского наложения текстуры, изображенной на рис. 2.18 на куб.

Рис. 2.19. Плоское наложение текстуры

Этот метод часто применяется для больших объектов, особенно когда зритель может видеть только одну сторону объекта. Плоское наложение является простым в использовании, поскольку требует только задания направления наложения текстуры на объект. Так как при плоском наложении текстура накладывается на объект только в одном направлении, боковые стороны объекта обычно получаются полосатыми.

Другой метод наложения называется цилиндрическим. При цилиндрическом наложении текстура сворачивается в цилиндр, внутри которого находится объект. Этот метод показан на рис. 2.20. Обратите внимание на шов в месте встречи краев текстуры.

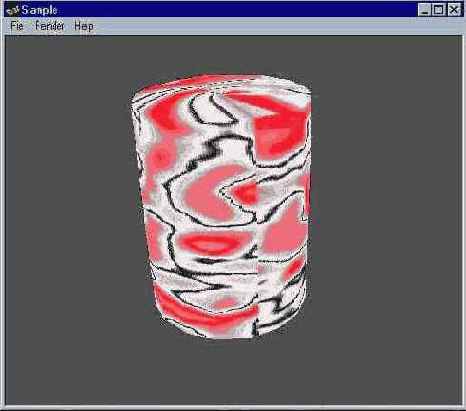
Рис. 2.20. Цилиндрическое наложение текстуры

Важно помнить, что способ наложения текстуры и форма покрываемого текстурой объекта совершенно не зависят друг от друга. Вы можете применять плоское наложение текстуры к сфере или сферическое наложение к кубу. Direct3D поддерживает плоский, сферический и цилиндрический методы наложения текстуры.

Более детальное обсуждение методов наложения текстур содержится в главе 5.

Техника удаления невидимых поверхностей

В трехмерной графике очень важно определить, какие объекты являются видимыми, а какие скрыты другими объектами. Визуализация сцены без учета того, какие поверхности расположены ближе зрителю и закрывают другие, приводит к получению неправильного изображения. Алгоритмы, которые решают эту проблему, называются методами удаления невидимых поверхностей. Существует много методов удаления невидимых поверхностей, каждый из которых имеет свои достоинства и недостатки. Метод, применяемый в Direct3D, называется Z-буферизацией.

Типы источников света

Источники света могут быть нескольких типов. Типичные источники света это рассеянный свет, точечное освещение и зональное освещение.

Точечное освещение

Точечный источник света (point light) излучает свет во всех направлениях. Точечный источник света имеет заданное местоположение, но не имеет ориентации. Точечное освещение требует значительного времени на вычисления, поскольку свет от источника распространяется во всех направлениях. Однако часто расход времени на вычисления бывает оправданным из-за реалистичных эффектов, которые создает точечное освещение. Иногда точечное освещение называют всенаправленным светом (omni или omni-directional light).

Трассировка лучей

Трассировка лучей (ray-tracing) позволяет получить наиболее реалистичное изображение по сравнению с любым другим методом визуализации. Действительно, трассировка лучей известна как способ получения фотореалистичных и даже гиперреалистичных изображений. Трассировка лучей использует метод полностью отличный от методов, которые мы обсудили ранее. Алгоритм трассировки лучей автоматически вычисляет тени, отражения и преломления (другие методы визуализации не выполняют эти вычисления).

К сожалению, трассировка лучей очень медленна. Для получения одного изображения могут потребоваться часы и даже дни. Разумеется, трассировка лучей не подходит для графики в реальном масштабе времени и не поддерживается Direct3D. На рис. 2.26 приведено изображение, полученное методом трассировки лучей (с помощью программы POV-Ray).

Рис. 2.26. Сцена, полученная методом трассировки лучей

Трехмерные системы координат

Целью трехмерной графики является получение двухмерного представления трехмерной сцены. Двухмерное представление необходимо, потому что поверхность, на которой изображается сцена — в нашем случае экран компьютера — является двухмерной. Итак, трехмерная графика требует создания двух представлений одной и той же сцены: трехмерного представления, которое остается невидимым и двухмерного представления, которое отображается на экране. Сначала мы поговорим о невидимом, трехмерном представлении.

Представление объекта в трех измерениях может быть выполнено с использованием системы координат, состоящей из трех отдельных осей. Эти оси обычно называются X, Y и Z.

Существует два варианта трехмерной системы координат: левосторонняя и правосторонняя. Различаются они направлением оси Z. В левосторонней системе удаленные от зрителя объекты имеют большее значение координаты Z, в то время как более близкие объекты имеют меньшее значение координаты Z. В правосторонней системе координат ось Z имеет противоположное направление: удаленные объекты характеризуются меньшим значением координаты Z, а более близким объектам соответствует большее значение Z. Direct3D использует левостороннюю систему координат, так что далее в главе мы будем использовать именно ее. Увидеть левостороннюю систему координат вы можете на рис. 2.1. Стрелки указывают направления, в которых значения координат вдоль осей увеличиваются.

Рис. 2.1. Трехмерная система координат

Любая точка в пространстве может быть определена набором из трех значений. Эти значения показывают позицию точки вдоль каждой из осей и указываются в этой книге в угловых скобках, например, <1, 2, 3>. Числа в примере определяют положение точки вдоль осей X, Y и Z соответственно.

Векторы

Вектор (vector), подобно точке, определяется тремя значениями, но вектор описывает направление и скорость, а не расположение в пространстве.

Возьмем для примера значения <0, 1, 0>. Если мы считаем эти числа описанием точки, тогда они указывают на место, расположенное на одну единицу выше начала координат (единицы выберите сами: сантиметры, мили, или что-то еще). Однако если мы считаем эти три числа описанием вектора, вместо местоположения мы получаем направление и скорость. В нашем случае направление — вверх и скорость 1. Представление векторов тройкой чисел несколько упрощено, поскольку в действительности для описания вектора необходимо шесть чисел: три для начальной точки и три для конечной. Это дает нам направление (ориентация второй точки относительно первой) и скорость (расстояние между двумя точками). Вектор может быть описан тремя числами, только если подразумевается, что его начальная точка совпадает с началом координат <0, 0, 0>.

Давайте взглянем на другой вектор: <2, 0, 0>. Этот вектор определяет направление вправо, потому что начинается в точке <0, 0, 0> и идет вправо вдоль оси X на две единицы. Поскольку вектор <2, 0, 0> представляется отрезком в два раза длиннее вектора <0, 1, 0>, скорость, определяемая вектором <2, 0, 0>, в два раза больше скорости, определяемой вектором <0, 1, 0>. На рис. 2.4 показаны два только что рассмотренных вектора.

Рис. 2.4. Вектор <0, 1, 0> и вектор <2, 0, 0>

Важно помнить, что векторы и точки — различные понятия. Точка определяет положение в пространстве, а вектор нет. Местоположение используется, чтобы определить вектор, но не наоборот (вектор не определяет местоположения). Векторы на рис. 2.4 расположены в начале координат, потому что они так представлены в цифровом виде, однако эти стрелки могли бы быть расположены в любом другом месте координатной системы.

Вершины

Вершины (vertices) представляют собой точки, которые используются для определения положения в трехмерном пространстве таких объектов, как грани и сетки (мы поговорим о гранях и сетках чуть позже). Вершины, подобно точкам, указывают местоположение, и сами невидимы. Однако Direct3D поддерживает режим, в котором вершины изображаются на экране точками. Этот режим имеет малое практическое значение, поскольку трудно оценить изображение, видя только вершины. Фактически, сцены нарисованные в этом режиме, напоминают головоломку в стиле «соедини все точки». (Великолепно — дайте мне карандаш!).

Вращение

Операция вращения позволяет нам изменить ориентацию объекта. Для вращения объекта требуется, чтобы мы определили ось вращения и угол поворота.

Мы можем использовать вектор, чтобы задать ось вращения, и числовое значение, чтобы указать, на сколько следует повернуть объект.

Итак, давайте вернемся к нашему исходному кубу и повернем его относительно оси Z на 45 градусов.

Вращение относительно оси Z означает, что куб повернется так, будто он проткнут осью Z и свободно поворачивается на ней только в одном направлении. Мы укажем это с помощью вектора <0, 0, 1> и числа 45. На рис. 2.16 показан результат выполнения этой операции вращения.

Рис. 2.16. Куб, повернутый на 45 градусов относительно оси <0, 0, 1>

Z-буферизация

Z-буферизация использует буфер памяти для того, чтобы определить, какие поверхности расположены ближе к зрителю. Значения Z, которые хранятся в этом буфере, не обязательно соответствуют оси Z; они содержат информацию о «глубине» расположения каждой грани по отношению к зрителю. По мере вывода граней значения координаты Z точек сравниваются со значениями координаты Z из буфера. Если значения в буфере указывают, что выводимая поверхность ближе к зрителю, чем любые существующие, то новая поверхность будет наложена на старые. Если новая поверхность расположена дальше, чем какая-либо из существующих, то она не выводится.

Скорость визуализации может быть увеличена при помощи сортировки поверхностей от ближних к дальним (front-to-back). Это повышает производительность, потому что сначала выводятся объекты на переднем плане сцены, а невидимые поверхности не будут затронуты вообще. К счастью для нас, абстрактный режим Direct3D выполняет Z-буферизацию (включая сортировку) без всякого вмешательства с нашей стороны.

Z-буферизация: За и Против

Z-буферизация — один из самых простых и самых быстрых методов удаления невидимых поверхностей. Она обеспечивает точность визуализации до пикселя (некоторым алгоритмам это недоступно) и эффективно обрабатывает сложные сцены. Главный недостаток Z-буферизации — значительный объем памяти, который требуется для Z-буфера. Z-буфер должен быть, по крайней мере, такого же размера, какой имеет выходное изображение, и быть 32-разрядным. Например, для программы, работающей в режиме 800x600 с 16-разрядным Z-буфером, требуется почти мегабайт памяти только для одного Z-буфера.

и отличаются друг от друга,