Катись, мяч, катись!
Как сделать так, чтобы сфера скатывалась с холма, а не соскальзывала с него?
Тема:
Анимация.
Используемые техники и инструменты:
Make Live (Сделать Активным), Curve on Surface (Кривая на Поверхности), Arc Measure Tool (Измерение Дуги).
Нет ничего сложного в том, чтобы передвинуть объект слева направо. Довольно просто толкать объект по горизонтальной плоскости. Однако совсем не так легко двигать объект по неровной поверхности, точно соблюдая заданный путь движения (использовать динамическую симуляцию в этом случае вы не можете: результаты могут быть самыми неожиданными). А если объект является сферой, которая должна катиться, а не скользить, - тут есть над чем задуматься. Но давайте отложим размышления на потом и начнем двигать куб по холмистой поверхности.

Рис. 7.1. Вот так выглядит реальный курвиметр для измерения длины кривой линии, например дороги на карте французских Альп
Задайте длительность анимации 400 кадров. Создайте NURBS-плоскость шириной 20 и плотностью 20x20 патчей в V и U направлениях. Нажмите клавишу F3, выберите Edit NURBS / Sculpt Surfaces (Редактирование NURBS / Создать Рельеф Поверхности) для деформации поверхности. Выделите поверхность и преобразуйте ее в «активный» объект. Для этого либо нажмите на пиктограмму с магнитом в верхней части экрана (рис. 7.2), либо выберите Modify / Make Live (Модифицировать / Сделать Активным). С этого момента вы можете работать прямо на поверхности.
Рис. 7.2. Пиктограмма с магнитом в верху окна Мауа позволяет вам работать непосредственно на поверхности
-
Выберите один из инструментов Create Curve (Создать Кривую) и постройте кривую. Для этого либо несколько раз щелкните мышкой по поверхности, добавляя к ней точки, либо проведите мышкой по поверхности, удерживая нажатой левую кнопку.
Выйдите из режима Live mode (режим Сделать Активным), нажав снова пиктограмму с магнитом.
Кривая, которую вы только что создали непосредственно на поверхности, и будет путем движения нашего куба.
Создайте полигональный куб. Нажмите клавишу 4, для того чтобы войти в режим Wireframe mode (режим Каркас). Выделите куб, а затем и кривую на поверхности. Создайте путь для движения куба. Для этого нажмите F2, выберите Animate / Motion Paths / Attach to Motion Path (Анимация / Пути Движения / Присоединить к Пути Движения) (рис. 7.3).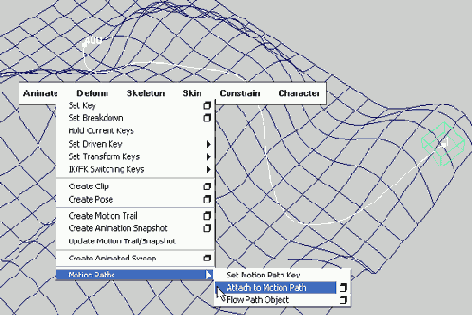
Рис. 7.3. Присоединим куб к кривой на поверхности
Когда вы воспроизведете анимацию, то увидите, как куб движется вниз и вверх по холмам. Есть, правда, одна проблема: когда куб скользит по поверхности, он погружается в нее (рис. 7.4).
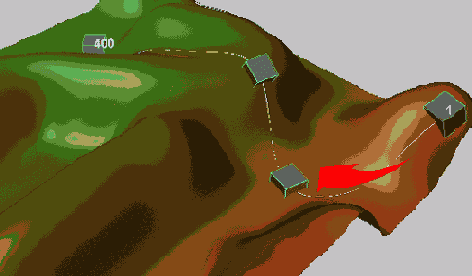
Рис. 7.4. Наш куб движется по холмам и по долинам (и проваливается в них)
Это связано с положением опорной точки куба. Мы могли бы передвинуть ее, однако вместо этого удалим куб и создадим NURBS-сферу. Давайте поговорим об опорной точке сферы. Если вы присоедините сферу к пути ее движения, как вы это уже делали с кубом, то ее нижняя часть тоже погрузится в поверхность. Если же вы опустите опорную точку сферы, для того чтобы избавиться от этого погружения, то сфера перестанет вращаться относительно своего центра - а это именно то, что необходимо для ее качения (а не скольжения) по поверхности.
Что нам тут действительно нужно, так это объединить два объекта в одном. Один будет отвечать за движение по заданному пути, а другой возьмет на себя качение сферы. Все это мы осуществим с помощью иерархической анимации - громкое слово для обозначения простой процедуры работы с группами, членами и родительскими объектами, сферу саму с собой и присоединить группу к пути движения. Единственный член группы - сфера - может теперь вращаться вокруг своей центральной точки, в то время как группа будет двигаться вверх и вниз по холмам. Группа несет в себе сферу, а сфера, в свою очередь, заботится об эффекте качения.
Сгруппируйте сферу саму с собой, используя клавиши клавиатуры Ctrl+g либо выбрав Edit / Group (Редактирование / Группа). Переименуйте группу. В режиме Insert (Режим редактирования опорной точки) переместите опорную точку группы к южному полюсу сферы (рис. 7.5).
Рис. 7.5. Перемещаем опорную точку группы сферы после группирования сферы с самой собой. Благодаря этому сфера остается на поверхности во время движения
-
Присоедините группу сферы - но не саму сферу! - к кривой на холмистой поверхности так же, как вы раньше делали это с кубом. Нажмите F2, выберите Animation / Motion Paths / Attach to Motion Path (Анимация / Пути Движения / Присоединить к Пути Движения).
Сфера движется по поверхности (не погружаясь в нее) (рис. 7.6). В действительности движется не сама сфера, а ее группа, которая, конечно, несет в себе сферу, куда бы ни двигалась. Если сфера склоняется к кривой пути движения, исправьте это, изменив внутреннюю ось пути. Откройте Attribute Editor (Редактор Атрибутов) motionPathl и установите Up Axis (Верхняя Ось) на Y.

Рис. 7.6. Скользим и съезжаем с холмов - но не катимся
Теперь можно приступить к качению. Как предотвратить скольжение сферы? Мы заставим ее вращаться внутри группы для создания впечатления качения. Если мы поделим длину кривой на длину окружности сферы, то узнаем, сколько раз ей нужно повернуться вокруг своей оси за время движения по поверхности. Радиус сферы равен 1. Формула вычисления длины окружности следующая:
2*Radius*p.
Итак, длина окружности нашей сферы составляет: 2 * 1 * 3.14 = 6.28.
Таким образом, каждый раз, когда сфера преодолеет 6,28 единицы и выполнит один полный оборот, выглядеть это будет так, будто она катится по поверхности, чувствуя трение с ней. Мауа предлагает пару весьма полезных способов для измерения расстояний. Тот, который потребуется нам для измерения длины нерегулярной кривой, называется Arc Length Tool (Длина Дуги).
Выберите Create / Arc Length Tool (Создать / Длина Дуги). В режиме Wireframe mode (Режим Каркас) щелкните мышкой по кривой. Инструмент показывает вам расстояние между началом кривой и точкой, на которую вы укажете курсором (рис. 7.7). Перетащите Arc Length Tool (Длина Дуги) в конец кривой и запомните появившееся значение.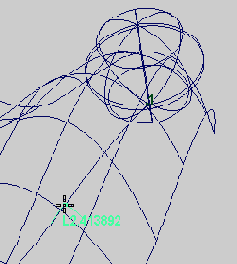
Рис. 7.7. Инструмент Arc Length Tool (Длина Дуги) измеряет длину дуги между началом кривой и любой точкой на ней
-
Разделите длину кривой на длину окружности сферы,
которая составляет 6,28.
В нашей анимации длина кривой составляет 25,54 единицы. 25 / 6,28 = 4,07.
Следовательно, сфера сделает вокруг своей оси 4 полных оборота.
-
Умножьте результат на 360.
Теперь вы знаете, на сколько градусов должна повернуться сфера, чтобы прокатиться по всему пути движения.
Идите в начало анимации. Выделите сферу (не группу!) и выберите направление вращения. Задайте ключевой кадр для этого параметра вращения. Идите в конец временной шкалы. В кадре 400 увеличьте значение вращения на число, которое вы получили в результате вычислений, и задайте еще один ключевой кадр (рис. 7.8).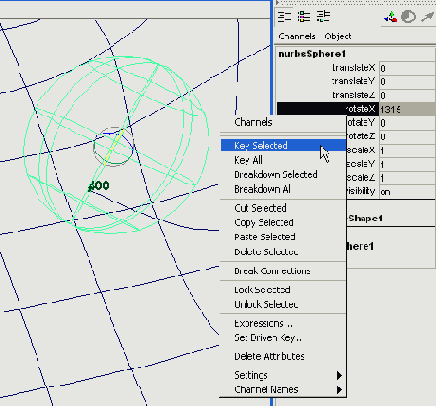
Рис. 7.8. После небольших вычислений вращение сферы получает второй ключевой кадр. В нашем случае она поворачивается на -1464 градусов вокруг оси Z
-
Откройте Graph Editor (Редактор Анимационных Кривых) и задайте для касательных вращения сферы тип Linear (Линейный) (рис. 7.9).
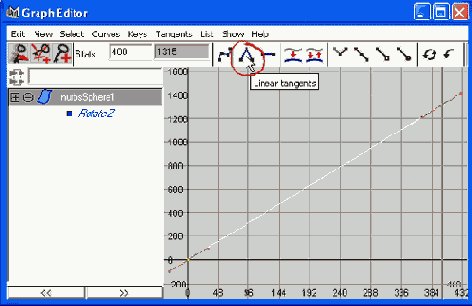
Рис. 7.9. Для того чтобы получить реалистичное перекатывание, для касательных должен быть задан тип Linear (Линейный), если он еще не задан
Если сфера вращается в противоположном направлении, переустановите ключевой кадр, на этот раз с отрицательным значением. При воспроизведении анимации вы увидите сферу, плавно катящуюся по своему извилистому пути (см. рис. 7.10).

Рис. 7.10. Сфера реалистично катится по извилистому пути
Этот способ позволяет вам получить за короткое время вполне реалистичное качение сферы, однако он не очень удобен. Если, например, хоть один параметр - радиус сферы или длина пути - меняется, эффект качения пропадет, и вам снова придется производить вычисления и переустанавливать второй ключевой кадр. Для того чтобы полностью контролировать ситуацию, вам придется создать выражения, которые будут использовать значения этих параметров как переменные.
У нашей анимации есть еще одно слабое место: сфера катится слишком монотонно. Например, она не ускоряется при движении вниз с холма. Это можно исправить путем установления большего количества ключевых кадров для U Value (Значения U) пути движения и вращения сферы. После этого вам нужно будет дополнительно настроить две соответствующие анимационные кривые в Graph Editor (Редактор Анимационных Кривых).
А теперь кое-что новенькое. Использовали ли вы когда-нибудь Тот Kluysken's Caustics при рендеринге рубинового колье?