Буфер глубины
Если теперь мы попытаемся выводить объекты сцены, то они будут рисоваться в том порядке, в котором воспроизводятся. При этом нарисованные позже примитивы будут "лежать" поверх ранее выведенных. Для адекватной визуализации трехмерных объектов в графических библиотеках предусмотрен так называемый буфер глубины или z-буфер, который представляет собой двумерный массив, хранящий для каждого растеризуемого пикселя значение координаты z. Рассмотрим принцип работы буфера глубины на примере левосторонней системы координат. В начале в z-буфер заносятся (очищается) максимально возможные значения z, а буфер регенерации заполняется значениями пикселей, соответствующими фону. Затем каждая грань объекта преобразуется в растровую форму, причем порядок растеризации грани не играет особой роли. При разложении многоугольника в растр для каждой его точки выполняются следующие шаги:
Вычисление глубины (z-координаты) в точке (x,y);Если z(x,y) меньше чем значение в z-буфере в позиции (x,y) то в z-буфер заносится значение z-координаты растеризуемой точки, а в буфер регенерации помещается обрабатываемый пиксель.
Если выполняется условие шага 2, это означает, что точка многоугольника расположена ближе к наблюдателю, чем точка, значение яркости которой находится в данный момент в позиции (x,y) буфера регенерации.
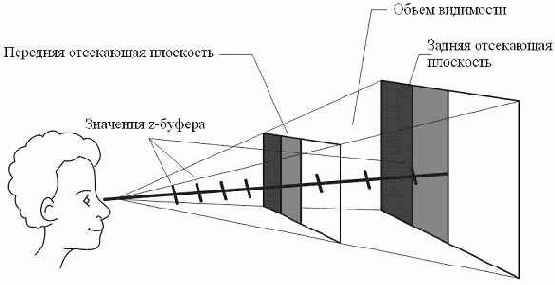
Единственный недостаток рассмотренного алгоритма – необходимость дополнительной памяти для хранения z-буфера, однако простая и эффективная реализация позволяет использовать этот алгоритм во многих приложениях. Для инициализации буфера глубины в библиотеке Direct3D достаточно заполнить два поля структуры D3DPRESENT_PARAMETERS:
| C++ | D3DPRESENT_PARAMETERS params; … ZeroMemory( ¶ms, sizeof(params) ); … params.EnableAutoDepthStencil = true; params.AutoDepthStencilFormat = D3DFMT_D16; … | |
| Pascal |
var params: TD3DPresentParameters; … ZeroMemory( @params, SizeOf(params) ); … params.EnableAutoDepthStencil := true; params.AutoDepthStencilFormat := D3DFMT_D16; … |
Программист может не беспокоиться о линейных размерах буфера глубины, т.к.
система автоматически определяет размеры. Для работы с буфером глубины необходимо также установить константу режима D3DRS_ZENABLE в значение "истина".
| C++ | device->SetRenderState (D3DRS_ZENABLE, D3DZB_TRUE); |
| Pascal | device.SetRenderState(D3DRS_ZENABLE, 1); |
| C++ | device->SetRenderState (D3DRS_ZENABLE, D3DZB_FALSE); |
| Pascal | device.SetRenderState(D3DRS_ZENABLE, 0); |
| C++ | device->Clear( 0, 0, D3DCLEAR_TARGET | D3DCLEAR_ZBUFFER, D3DCOLOR_XRGB(255,255,255), 1.0f, 0 ); |
| Pascal | device.Clear( 0, nil, D3DCLEAR_TARGET or D3DCLEAR_ZBUFFER, D3DCOLOR_XRGB(255,255,255), 1.0, 0 ); |
Принципы построения трехмерной сцены
В трехмерной графике пространственные объекты, заданные в непрерывном виде, как правило, аппроксимируют (приближают) множеством треугольников. Именно треугольник представляет собой элементарный примитив, с помощью которого описываются все элементы сцены, в том числе и те, которые имеют гладкую форму (сфера, цилиндр, параметрические поверхности и др.).
Процесс формирования изображения должен учитывать две главные сущности. Это визуализируемый объект сцены и наблюдатель. Объект существует в пространстве независимо от кого-либо. Наблюдатель же представляет собой средство формирования изображения наблюдаемых объектов. Именно наблюдатель формирует изображение. Наблюдатель и наблюдаемый объект существуют в одном и том же трехмерном мире, а создаваемое при этом изображение получается двухмерным. Суть процесса формирования изображения состоит в том, чтобы, зная положение наблюдателя и положение объекта, описать (синтезировать) получаемое при этом двухмерное изображение (проекцию).
В большинстве графических библиотек присутствуют следующие сущности трехмерной сцены:
объекты;наблюдатель (камера);источники света;свойства материалов объекта.
При этом моделируемая трехмерная сцена может описываться тысячами, а иногда миллионами вершин. Для каждой вершины (точки) примитива должны выполняться вычисления по одним и тем же формулам.
Как мы знаем, точка в 3D графике задается, как правило, набором из 4-х значений (x,y,z,w). Реальные координаты точки в пространстве будут (x/w, y/w, z/w), компонент w является масштабом. Обычно для точек w=1. Вектор – направленный отрезок. Вектора равны если у них одинаковая длина и направление. Вектора также задаются в виде линейного массива 1х4 (x,y,z,w), но компонент w у векторов равен 0. Для выполнения преобразований с вершинами используют матричный подход. Матрица размерности MxN – прямоугольная таблица, имеющая M строк, N столбцов и заполненная элементами одного типа. В 3D графике используют, как правило, матрицы размерности 4х4. Таким образом преобразование точки в пространстве сводится к умножению вектор-строки размерности 4 на матрицу преобразования размером 4х4:

Так, например, умножение всех вершин объекта на одну из матриц вращения приведет к вращению этого объекта вокруг оси Ox, Oy или Oz соответственно. Для сложного трансформации объекта можно использовать последовательные преобразования, которые выражаются в перемножении (конкатенации) соответствующих матриц элементарных преобразований. Таким образом, можно сначала рассчитать единую (общую) матрицу преобразования (перемножить между собой все элементарные матрицы трансформации), а затем использовать только ее. Так, например, вращение объекта вокруг совей оси и одновременное движение по кругу определенного радиуса, может быть описано следующей последовательностью матриц: Vi *MatRot1(…)*MatTrans(…)*MatRot2(…), где Vi – координаты вершин объекта, MatRot1 – матрица поворота вокруг совей оси, MatTrans – матрица перемещения, MatRot2 – матрица вращения по кругу.
Вам не придется самостоятельно запоминать и вычислять все матрицы преобразования "вручную", т.к. во всех библиотеках 3D графики они предусмотрены. В библиотеке Direct3D определен матричный тип D3DXMATRIX – это структура, которая содержит 4х4 элементов.
Элемент матрицы с индексами ij указывает на значение, хранящееся в строке с номером i и столбце с номером j. Например, элемент _32 указывает на значение m[3][2]. Обращаться к элементам матрицы (читать, записывать) можно двумя способами.
| C++ | D3DXMATRIX m; m._11 = …; или m.m[1][1] = …; |
| Pascal | var m: TD3DXMatrix; … m._11 := …; или m.m[1,1] = …; |
| C++ | D3DXMATRIX m; // Создание единичной матрицы D3DXMatrixIdentity(&m); // Создание матрицы перемещения D3DXMatrixTranslation(&m, dx, dy, dz); // Создание матрицы масштабирования D3DXMatrixScaling(&m, kx, ky, kz); // Создание матриц вращения D3DXMatrixRotationX(&m, angleX); D3DXMatrixRotationY(&m, angleY); D3DXMatrixRotationZ(&m, angleZ); |
| Pascal | var m: TD3DXMatrix; // Создание единичной матрицы D3DXMatrixIdentity(m); // Создание матрицы перемещения D3DXMatrixTranslation(m, dx, dy, dz); // Создание матрицы масштабирования D3DXMatrixScaling(m, kx, ky, kz); // Создание матриц вращения D3DXMatrixRotationX(m, angleX); D3DXMatrixRotationY(m, angleY); D3DXMatrixRotationZ(m, angleZ); |
При работе с матрицами следует учитывать, что преобразования масштабирования и вращения производятся относительно начала координат. Для комбинирования (умножения) двух матриц существует функция D3DXMatrixMultiply(), которая помещает результат перемножения двух матриц, которые передаются в качестве второго и третьего аргументов, в первый. К примеру, мы хотим повернуть объект вокруг оси Oy на угол 30 градусов и переместить его на вектор (1,2,3). Для этого можно воспользоваться правилом композиции двух элементарных преобразований с помощью матрицы поворота и матрицы перемещения.
| C++ | D3DXMATRIX matRotY, matTrans, matRes; D3DXMatrixRotationY( &matRotY, 30*D3DX_PI/180 ); D3DXMatrixTranslation( &matTrans, 1, 2, 3 ); D3DXMatrixMultiply(&matRes, &matRotY, &matTrans); |
| Pascal | var matRotY, matTrans, matRes: TD3XDMatrix; D3DXMatrixRotationY( matRotY, 30*pi/180 ); D3DXMatrixTranslation( matTrans, 1, 2, 3 ); D3DXMatrixMultiply( matRes, matRotY, matTrans ); |
| C++ | D3DXMATRIX matRotY, matTrans; D3DXMatrixRotationY( &matRotY, … ); D3DXMatrixTranslation( &matTrans, … ); device->SetTransform(D3DTS_VIEW, D3DXMatrixMultiply(NULL, &matRotY, &matTrans)); |
| Pascal | var matRotY, matTrans, matRes: TD3XDMatrix; D3DXMatrixRotationY( matRotY, … ); D3DXMatrixTranslation( matTrans, … ); device.SetTransform(D3DTS_VIEW, D3DXMatrixMultiply(nil, matRotY, matTrans)^); |
Моделируемые объекты трехмерного мира (сцены);Положение виртуальной камеры, которая определяет перспективу.
В терминах систем координат процесс получения проекции может быть описан следующей упрощенной блок схемой:
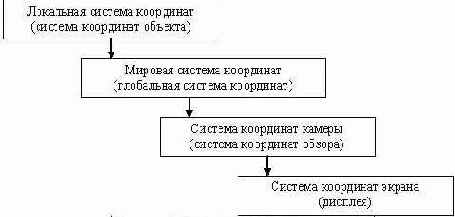
Как известно из курса линейной алгебры, переход от одной системы координат к другой эквивалентен смене базиса. Когда нужно преобразовать объект из одного базиса в другой, нужно умножить все вершины объекта на соответствующую матрицу приведения базиса.
Библиотека Direct3D позволяет работать как в левосторонней системе координат, так и в правосторонней. Далее будем рассматривать все примеры для левосторонней системы координат.
Локальная система координат (локальное пространство) определяет исходные координаты объекта, т.е. в тех в которых он задан. Моделирование объекта в локальной (собственной) системе координат удобнее, чем напрямую в мировой системе координат. Локальная система позволяет описывать объект, не обращая внимания на положение, размер, ориентацию других объектов в мировой системе координат.
После того как заданы все объекты в своих собственных (локальных) системах координат, необходимо привязать их к общей мировой системе координат. Процесс трансформации координат объектов, заданных в локальных системах в мировую (общую) называют мировым преобразованием (world transform). Обычно используют 3 типа преобразований: перемещение, масштабирование, вращение. Мировое преобразование описывается с помощью матрицы, используя метод SetTransform интерфейса IDirect3DDevice9. Для применения мирового преобразования метод SetTransform вызывается с параметром D3DTS_WORLD. Предположим, что у нас в сцене присутствуют два объекта: куб и сфера. Мы собираемся отобразить куб в точке с координатами (-3, 2, 6), а сферу в точке (5, 0, -2) мировой системы координат. Это можно проделать с помощью следующих шагов.
| C++ | D3DXMATRIX matCube, matSphere; D3DXMatrixTranslation(&matCube, -3.0f, 2.0f, 6.0f); pDirect3DDevice->SetTransform(D3DTS_WORLD, &matCube); drawCube(); D3DXMatrixTranslation(&matSphere, 5.0f, 0.0f, -2.0f); pDirect3DDevice->SetTransform(D3DTS_WORLD, &matSphere); drawShepre(); |
| Pascal | var matCube, matSphere: TD3DXMatrix; … D3DXMatrixTranslation(matCube, -3.0, 2.0, 6.0); device.SetTransform(D3DTS_WORLD, matCube); drawCube; D3DXMatrixTranslation(matShpere, 5.0, 0.0, -2.0); device.SetTransform(D3DTS_WORLD, matSphere); drawShepre; |
Построение проекции весьма сложная и очень неэффективная операция когда камера имеет произвольное положение и направление в мировой системе координат. Чтобы упростить эту ситуацию, мы перемещаем камеру в начало мировой системы координат и поворачиваем ее так, чтобы "взгляд" камеры был направлен в положительную сторону оси Z, как показано на рисунке ниже.
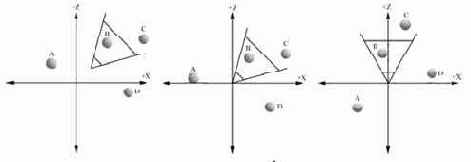
Матрица перехода в систему координат камеры может быть получена с помощью функции D3DXMatrixLookAtLH(), прототип которой показан ниже:
D3DXMatrixLookAtLH ( matView, // результат Eye, // положение камеры в мировой системе координат At, // точка в мировой системе, куда направлена камера (взгляд) Up // вектор, указывающий "где верх" в мировой системе координат ).
Для установки матрицы вида (преобразование в пространство камеры) используется метод SetTransform с первым параметром D3DTS_VIEW.
Например, поместить камеру в точку (0,0,-3) и направить "взгляд" наблюдателя в начало системы координат, можно с помощью такого кода:
| C++ | D3DXMATRIX matView; D3DXVECTOR3 positionCamera, targetPoint, worldUp; positionCamera = D3DXVECTOR3(0,0,-3); targetPoint = D3DXVECTOR3(0,0,0); worldUp = D3DXVECTOR3(0,1,0); D3DXMatrixLookAtLH(&matView, &positionCamera, &targetPoint, &worldUp); device->SetTransform(D3DTS_VIEW, &matView); |
| Pascal | var matView: TD3DMatrix; positionCamera, targetPoint, worldUp : TD3DXVector3; … positionCamera := D3DXVector3(0, 0, -3); targetPoint := D3DXVector3(0, 0, 0); worldUp := D3DXVector3(0, 1, 0); D3DXMatrixLookAtLH(matView, positionCamera, targetPoint, worldUp); device.SetTransform(D3DTS_VIEW, matView); |
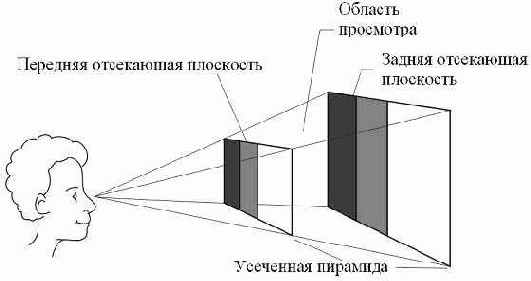
Последним этапом преобразования при получении 2D изображения является операция проекции. Библиотека поддерживает работу как с перспективной, так и с ортогональной проекциями.
Для работы с первым типом проекций предназначена функция D3DXMatrixPerspectiveFovLH(), для ортогональных же проекций нужна функция D3DXMatrixOrthoOffCenterLH(). Мы рассмотрим примеры работы с перспективной проекцией. Матрица перспективной проекции задает положение передней и задней отсекающих плоскостей, искажения, имитирующие перспективу. Прототип функции D3DXMatrixPerspectiveFovLH() приведен ниже.
D3DXMatrixPerspectiveFovLH( matProj, // результат fov, // вертикальный угол обзора aspect, // отношение ширины окна к высоте zn, // расстояние до передней отсекающей плоскости zf // расстояние до задней отсекающей плоскости )
Ниже приведены иллюстрации, которые поясняют значение последних четырех аргументов данной функции.
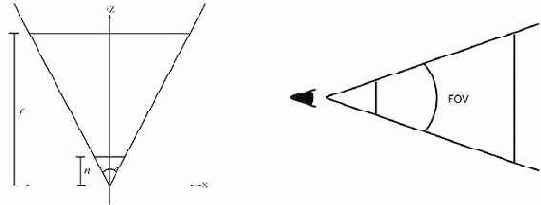
Для установки перспективной матрицы необходимо вызвать метод SetTransform с первым параметром D3DTS_PROJECTION. Приведенный ниже пример, создает и устанавливает матрицу проекции со следующими параметрами: вертикальный угол обзора – 45 градусов, расстояние до передней и задней отсекающих плоскостей – 1 и 100 единиц соответственно.
| C++ | D3DXMATRIX matProj; D3DXMatrixPerspectiveFovLH(&matProj, D3DX_PI/2, width/height, 1, 100); device->SetTransform(D3DTS_PROJECTION, &matProj); |
| Pascal | var matProj: TD3DXMatrix; D3DXMatrixPerspectiveFovLH(matProj, pi/2, Width/Height, 1, 100); device.SetTransform(D3DTS_PROJECTION, matProj); |
Таким образом, конвейер преобразований вершин объекта может быть описан следующей блок-схемой:
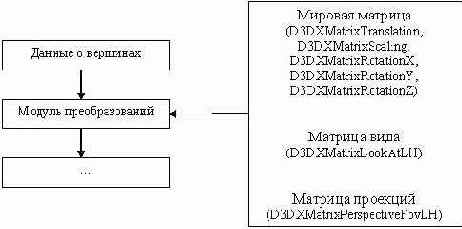
Каждая вершина трехмерной сцены подвергается следующему преобразованию V' = V*matWorld*matView*matProj, где V – исходная вершина, V' - преобразованная вершина.
Схема графического конвейера
В данном разделе мы рассмотрим принципы построения трехмерных сцен с помощью графической библиотеки Direct3D. Вначале необходимо познакомиться со схемой работы графического конвейера. Графический конвейер представляет собой некое аппаратно-программное устройство, которое переводит объекты, описанные в трехмерном пространстве XYZ, с учетом положения наблюдателя, во множество пикселей на экране вашего монитора. Ниже приведена блок-схема работы графического конвейера.
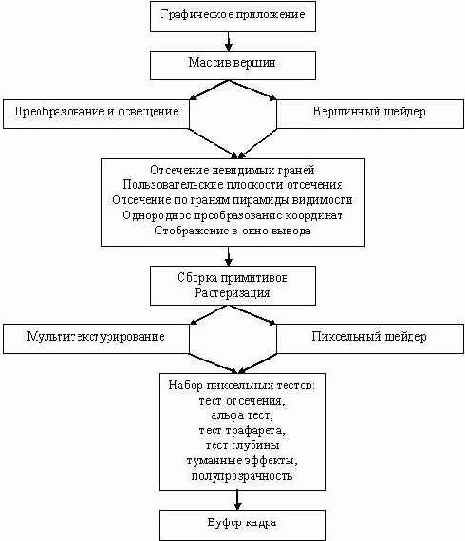
"Жизнь" вершин начинается, когда они попадают в графический конвейер из приложения. На первом шаге графического конвейера все вершины объектов подвергаются аффинным преобразованиям - вращению, масштабированию и перемещению. За этот шаг отвечает блок трансформации и освещения либо же вершинный шейдер. По сути, выполняют они одну и ту же работу по преобразованию вершин, но блок трансформации и освещения жестко задает правила обработки, в то время как вершинный шейдер является программируемым элементом на данной стадии. Здесь же происходит расчет освещенности в вершинах в зависимости от количества, места положения и типа источников света. Вершинный шейдер получает на вход одну вершину, содержащую координаты в локальной системе координат, и выдает ее же, но уже трансформированную в координатах системы наблюдателя (камеры).
Отсечение невидимых граней "удаляет" все треугольники сцены, которые расположены нелицевыми сторонами к камере (наблюдателю). Программист может указать порядок обхода вершин треугольника (по часовой/против часовой стрелки), при котором библиотека будет блокировать вывод этих примитивов.
Пользователь может установить дополнительные плоскости отсечения, которые будут отсекать те вершины и треугольники, которые находятся в отрицательном полупространстве плоскостей.
Отсечение по видимому объему задает пирамиду видимости, и примитивы, которые находятся вне этой пирамиды, будут отсекаться.
На следующем шаге графического конвейера производится так называемое однородное преобразование, при котором x,y,z координаты вершин делятся на четвертую компоненту, называемую однородным множителем.
После этого преобразования координаты треугольников будут нормализованы, а объем (пирамида) видимости трансформируется в единичный ортогональный куб.
Теперь нормализованные координаты отображаются в пространство экрана. На этом шаге "жизнь" вершин в графическом конвейере заканчивается.
Следующий этап начинается с растеризации треугольников и получении из них массива пикселей. Причем каждый растеризуемый пиксель обладает теми же атрибутами (цвет, текстурные координаты и т.д.) что и вершина после обработки вершинным шейдером. Значения же атрибутов пикселя вычисляются на основе линейной интерполяции вершин примитива.
Шаг мультитекстурирования может производиться либо с помощью механизма работы с текстурами, либо же с помощью пиксельных шейдеров. Пиксельные шейдеры можно рассматривать как некий программируемый механизм обработки пикселей. Причем способ и результат такой обработки зависит только от программиста. Именно с помощью пиксельных шейдеров получают визуальные эффекты, сравнимые с киноэффектами (моделирование воды, травяной поверхности, меха, микрорельефное и попиксельное освещение и др.).
После блока мультитекстурирования наступает фаза различных тестов, после успешного прохождения которых, пиксель попадает в буфер кадра (место в видеопамяти) и отображается на экране либо в заменяющую его текстуру.
Вывод трехмерных объектов
В первую очередь при визуализации трехмерных объектов, необходимо изменить формат вершины и набор FVF флагов.
| C++ |
struct VERTEX3D { FLOAT x, y, z; … }; VERTEX3D data[]; #define MY_FVF (D3DFVF_XYZ | …); |
| Pascal |
type Vertex3D = packed record x, y, z: Single; … end; const MY_FVF = D3DFVF_XYZ or …; var data: array of Vertex3D; |
Единственное отличие от двумерного случая будет заключаться в наличии операций с матрицами для преобразования объектов. Функции для визуализации трехмерных объектов будут такими же, какие мы использовали в двумерном случае: DrawPrimitive, DrawPrimitiveUP, DrawIndexedPrimitive, DrawIndexedPrimitiveUP. В качестве примера разберем построение, вращающего вокруг одной из координатных осей, цветного треугольника. Запишем шаги, которые мы должны проделать.
Определение формата вершин треугольника и набор FVF флагов;Заполнение массива вершин данными;Установка видовой и проекционной матриц;Установка мировой матрицы (поворот вокруг оси) и вывод примитива.
Приведем программные строки для каждого шага алгоритма.
| C++ |
struct VERTEX3D { FLOAT x, y, z; DWORD color; }; #define MY_FVF (D3DFVF_XYZ | D3DFVF_DIFFUSE); ... VERTEX3D points[3] = { { -1.0f,-1.0f, 0.0f, 0x00ff0000, }, { 0.0f, 1.0f, 0.0f, 0x0000ff00, }, { 1.0f,-1.0f, 0.0f, 0x000000ff, } } ... D3DXMATRIX matWorld, matView, matProj; D3DXMatrixLookAtLH( &matView, &D3DXVECTOR3 ( 0.0f, 0.0f,-5.0f ), &D3DXVECTOR3 ( 0.0f, 0.0f, 0.0f ), &D3DXVECTOR3 ( 0.0f, 1.0f, 0.0f ) ); device->SetTransform( D3DTS_VIEW, &matView ); D3DXMatrixPerspectiveFovLH( &matProj, D3DX_PI/4, 1.0f, 1.0f, 100.0f ); device->SetTransform( D3DTS_PROJECTION, &matProj ); ... D3DXMatrixRotationY( &matWorld, angle ); device->SetTransform( D3DTS_WORLD, &matWorld ); device->DrawPrimitive( D3DPT_TRIANGLELIST, 0, 1 ); |
| Pascal |
type Vertex3D = packed record x, y, z: Single; color: DWORD; end; const MY_FVF = D3DFVF_XYZ or D3DFVF_DIFFUSE; var points: array [0..2] of Vertex3D = ( (x: -1; y: -1; z: 0; color: $000000ff), (x: 0; y: 1; z: 0; color: $0000ff00), (x: 1; y: -1; z: 0; color: $00ff0000) ); matWorld, matView, matProj: TD3DMatrix; ... D3DXMatrixLookAtLH(matView, D3DXVector3(0,0,-5), D3DXVector3(0,0,0), D3DXVector3(0,1,0)); device.SetTransform(D3DTS_VIEW, matView); D3DXMatrixPerspectiveFovLH(matProj, PI/4, 1, 1, 100); device.SetTransform(D3DTS_PROJECTION, matProj); ... D3DXMatrixRotationY(matWorld, angle); device.SetTransform(D3DTS_WORLD, matWorld); device.DrawPrimitive(D3DPT_TRIANGLELIST, 0, 1); |
Ниже приведен пример нескольких кадров из анимации.
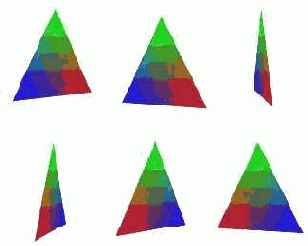
Библиотека Direct3D располагает механизмом отсечения граней. Идея заключается в том, что можно указать порядок обхода вершин треугольника (по часовой или против часовой стрелки) и отключить вывод тех граней, которые перечислены, например, по часовой стрелке. По умолчанию механизм отсечения граней отключен, т.е. воспроизводятся обе стороны примитива. Программно отключение "задних" сторон примитива реализуется через вывоз метода SetRenderState(D3DRS_CULLMODE, <значение>) интерфейса IDirect3DDevice9. В качестве второго параметра может выступать одна из трех констант: D3DCULL_NONE – механизм отбраковки граней выключен;
D3DCULL_CW – отбраковываются грани, вершины которых перечислены по часовой стрелке;
D3DCULL_CCW – отбраковываются грани, вершины которых перечислены против часовой стрелки.
Так, на представленном ниже рисунке грань (треугольник) задается перечислением своих вершин: v0, v1, v2 – по часовой стрелке; v0, v2, v1 – против часовой стрелки.

Освещенность и материалы
Для построения реалистичного изображения недостаточно только удалить невидимые грани объекта. После того как скрытые поверхности удалены, все видимые грани объекта необходимо закрасить, учитывая источники света, характеристики поверхностей, а также взаимное расположение и ориентацию поверхностей и источников света. В компьютерной графике выделяют, как правило, три типа источников света: точечный, параллельный и прожекторный. Более сложным с точки зрения моделирования, но зато более реалистичным источником света является точечный, при использовании которого освещенность поверхности зависит от ее ориентации: если лучи направлены перпендикулярно к поверхности, то она освещена максимально ярко, если же под углом, то освещенность ее убывает. Чем меньше угол падения лучей, тем меньше освещенность. Световая энергия, падающая на поверхность объекта, может быть поглощена, отражена или пропущена. Мы видим объект только благодаря тому, что он отражает или пропускает свет; если же объект поглощает весь падающий свет, то он невидим и называется абсолютно черным телом.
При расчете освещенности грани в компьютерной графике учитывают следующие типы отражения света от поверхности: рассеянное, диффузное, зеркальное. Интенсивность освещения граней объектов рассеянным светом считается постоянной в любой точке пространства. Это обусловлено тем, что рассеянный свет создается многочисленными отражениями от различных поверхностей пространства. Такой свет практически всегда присутствует в реальной обстановке. Даже если объект защищен от прямых лучей, исходящих от точечного источника света, он все равно будет виден из-за наличия рассеянного света. Интенсивность рассеянного света выражается как



При наличии в сцене точечного источника света, интенсивность диффузного отражения пропорциональна косинусу угла между нормалью к поверхности и направлением на источник света.
В этом случае для вычисления интенсивности диффузного отражения применяют закон косинусов Ламберта:





Свойством диффузного отражения является равномерность по всем направлениям отраженного света. Поэтому такие объекты имеют одинаковую яркость, вне зависимости от угла обзора. К примеру, матовые поверхности обладают таким свойством. Предположим, что у нас имеется два полигона, одинаково ориентированы относительно источника света, но расположенные на разных расстояниях от него. Если вычислить значения интенсивностей освещенности для каждого полигона, по приведенной формуле, то они окажутся одинаковыми. Это означает, что объекты, расположенные на разном расстоянии от источника света, будут освещаться независимо от их местоположения в трехмерной сцене. В этом случае интенсивность света должна быть обратнопропорциональна квадрату расстояния от источника до грани объекта. Тогда объект, расположенный дальше от источника будет темнее. Тем не менее на практике, как правило, используют не квадрат расстояния, а линейное затухание. В этом случае формула общей интенсивности может быть записана как:


Зеркальное отражение можно получить от любой блестящей поверхности. Осветите ярким светом обычное яблоко, и световой блик возникнет в результате зеркального отражения, а свет, отраженный от остальной части яблока, появится вследствие диффузного отражения. Следует отметить, что в том месте, где находится световой блик, яблоко будет казаться не красным, а, скорее всего – белым, т.е. окрашенным в цвет падающего света. Если изменить положение наблюдателя, то световой блик тоже сместится.
Это объясняется тем, что блестящие поверхности отражают свет неодинаково по всем направлениям. От идеально зеркальной поверхности свет отражается только в том направлении, для которого углы падения и отражения совпадают. Зеркально отраженный свет можно будет увидеть, если угол между вектором отражения (на рисунке обозначен R) и вектором наблюдения (на рисунке обозначен S) равен нулю.

Для неидеальных отражающих поверхностей интенсивность отраженного света резко падает с ростом









Таким образом, интенсивность грани складывается из трех составляющих: рассеянного света, диффузного света и зеркального света. Формула расчета общей интенсивности с учетом расстояния от наблюдателя до освещенной грани и трех составляющих света записывается как

Для более реалистичного отображения объектов сцены в библиотеке Direct3D определены понятия материал и свет. Материал в Direct3D задает свойства поверхности отображаемых примитивов. С помощью материала определяется как будет отражаться от поверхности примитива свет. Материал и свет (в контексте Direct3D) используются совместно. Одно без другого работать не будет.
Для работы с материалом предусмотрен специальный тип данных D3DMATERIAL9, который содержит следующие поля.
| C++ | typedef struct _D3DMATERIAL9 { D3DCOLORVALUE Diffuse; {рассеянный свет, исходящий от материала} D3DCOLORVALUE Ambient; {определяет окружающий свет} D3DCOLORVALUE Specular; {определяет отражающий (зеркальный) свет} D3DCOLORVALUE Emissive; {определяет излучающий свет материала} float Power; {мощность отражения} } D3DMATERIAL9; |
| Pascal | TD3DMaterial9 = packed record Diffuse: TD3DColorValue; {рассеянный свет, исходящий от материала} Ambient: TD3DColorValue; {определяет окружающий свет} Specular: TD3DColorValue; {определяет отражающий (зеркальный) свет} Emissive: TD3DColorValue; {определяет излучающий свет материала} Power: Single; {мощность отражения} end; |
Задавая параметры структуры D3DMATERIAL9, тем самым мы определяем свойства поверхности отображаемого объекта. Процесс создания и использование (назначение) материала включает в себя следующие шаги:
Объявление переменной типа D3DMATERIAL9;Заполнение соответствующих полей данной структуры;Установка материала.
Программно эти шаги реализуются таким образом:
| C++ | D3DMATERIAL9 material; ZeroMemory( &material, sizeof(D3DMATERIAL9) ); material.Diffuse=D3DXCOLOR(0.7f, 0.0f, 0.0f, 0.0f); material.Ambient=D3DXCOLOR(0.2f, 0.0f, 0.0f, 0.0f); material.Specular=D3DXCOLOR(0.1f, 0.0f, 0.0f, 0.0f); ... device->SetMaterial( &material ); |
| Pascal | var material: TD3DMaterial9; ... ZeroMemory(@material,SizeOf(TD3DMaterial9)); material.Diffuse:=D3DXColor(0.7, 0, 0, 0); // r, g, b, a material.Ambient:=D3DXColor(0.2, 0, 0, 0); material.Specular:=D3DXColor(0.1, 0, 0, 0); ... device.SetMaterial(material); |
Параллельный (направленный) – этот тип не имеет определенного источника света, он как бы повсюду, но светит в одном направлении.

Точечный – источник, светящий во всех направлениях (лампочка).
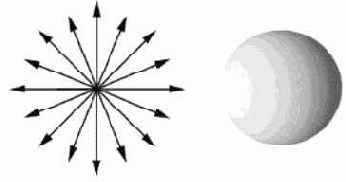
Прожекторный (нацеленный) – тип, имеющий определенный источник света, но светящий в заданном направлении в виде направленного конуса (фонарик).
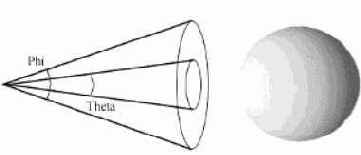
Свет в Direct3D состоит из трех составляющих: рассеянного, окружающего, зеркального, которые независимо друг от друга принимают участие в вычислении освещения граней. Они напрямую взаимодействуют с тремя цветами, определенными в свойствах материала. Результат такого сочетания (взаимодействия) и есть конечный цвет освещения сцены. В сценах Direct3D могут присутствовать до восьми различных по свойствам источников света. Для инициализации источника света в Direct3D необходимо проделать следующие шаги:
Объявить переменную типа D3DLIGHT9;Указать тип источника и заполнить необходимые поля данной структуры;Включить (разрешить) освещенность в сцене;Установить источники света;Включить источники света.
Структура D3DLIGHT9 содержит следующие поля:
| C++ | typedef struct _D3DLIGHT9 { D3DLIGHTTYPE Type; { тип источника света} D3DCOLORVALUE Diffuse; {рассеянный свет, излучающий источником} D3DCOLORVALUE Specular; {зеркальный свет, излучающий источником} D3DCOLORVALUE Ambient; {окружающий свет, излучающий источником} D3DVECTOR Position; {положение источника в сцене} для точечного D3DVECTOR Direction; {направление падающего света (вектор)} float Range; {максимальное расстояние освещения} для точечного float Falloff; {используется в прожекторном источнике} float Attenuation0; {определяют закон изменения освещения} float Attenuation1; {от параметра расстояния} float Attenuation2; {1/(A0+A1*D+A2*D^2), D–расстояние от источника} float Theta; {внутренний угол источника света} float Phi; {внешний угол, [0…pi]} } D3DLIGHT9; |
| Pascal | TD3DLight9 = packed record _Type: TD3DLightType; {тип источника света} Diffuse: TD3DColorValue; {рассеянный свет, излучающий источником} Specular: TD3DColorValue; {зеркальный свет, излучающий источником} Ambient: TD3DColorValue; {окружающий свет, излучающий источником} Position: TD3DVector; {положение источника в сцене} для точечного Direction: TD3DVector; {направление падающего света (вектор)} Range: Single; {максимальное расстояние освещения} для точечного Falloff: Single; {используется в прожекторном источнике} Attenuation0: Single; {определяют закон изменения освещения} Attenuation1: Single; {от параметра расстояния} Attenuation2: Single; {1/(A0+A1*D+A2*D^2), D–расстояние от источника} Theta: Single; {внутренний угол источника света} Phi: Single; {внешний угол, [0…pi]} end; |
D3DLIGHT_POINT, // точечный источник D3DLIGHT_SPOT, // источник-прожектор D3DLIGHT_DIRECTIONAL. // направленный источник
Ниже приведен пример установки направленного источника освещения в сцене.
| C++ | // создание и заполнение полей структуры, установка типа источника D3DLIGHT9 light; ZeroMemory(&light, sizeof(D3DLIGHT9) ); light.Type = D3DLIGHT_DIRECTIONAL; light.Diffuse = D3DXCOLOR(1.0f, 0.0f, 0.0f, 0.0f); light.Direction = D3DXVECTOR3(0.0f, 0.0f,1.0f); ... // разрешаем работы с освещенностью device->SetRenderState( D3DRS_LIGHTING, TRUE ); ... // установка и включение первого (и единственного) источника света device->SetLight( 0, &light ); device->LightEnable( 0, TRUE ); |
| Pascal | var light: TD3DLight9; ... // создание и заполнение полей структуры, установка типа источника ZeroMemory(@light,SizeOf(TD3DLight9)); light._Type:=D3DLIGHT_DIRECTIONAL; light.Diffuse:=D3DXColor(1,0,0,0); light.Direction:=D3DXVector3(0,0,1); // разрешаем работы с освещенностью device.SetRenderState(D3DRS_LIGHTING, 1); ... // установка и включение первого (и единственного) источника света device.SetLight(0,light); device.LightEnable(0,true); |
Но одних материалов и источников света недостаточно для того, чтобы объекты сцены были освещены. При использовании освещения необходимо определить нормаль к каждой грани трехмерного примитива. Нормаль представляет собой вектор, расположенный перпендикулярно одной их сторон выводимого примитива.
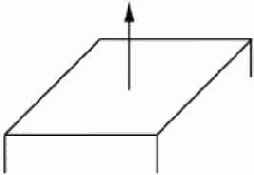
Именно с помощью нормалей рассчитывается освещенность объекта (граней). Как правило, нормали задаются в каждой вершине примитива.
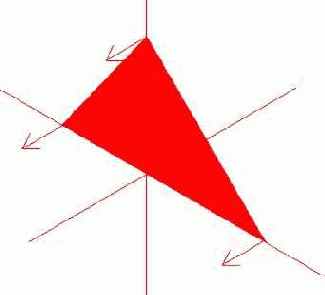
Поэтому необходимо корректно изменить формат вершин и набор FVF флагов.
| C++ | struct VERTEX3D { FLOAT x, y, z; FLOAT nx, ny, nz; }; VERTEX3D data[]; #define MY_FVF (D3DFVF_XYZ | D3DFVF_NORMAL); |
| Pascal | type Vertex3D = packed record x, y, z: Single; nx, ny, nz: Single; end; const MY_FVF = D3DFVF_XYZ or D3DFVF_NORMAL; var data: array of Vertex3D; |
| C++ | D3DXVECTOR3 direction = D3DXVECTOR3(0.0f, 0.0f,1.0f); D3DXVec3Normalize( (D3DXVECTOR3*)&light.Direction, &direction ); |
| Pascal | D3DXVec3Normalize( light.Direction, D3DXVector3(0, 0, 1) ); |
| C++ | device->SetRenderState(D3DRS_NORMALIZENORMALS, TRUE ); |
| Pascal | device.SetRenderState(D3DRS_NORMALIZENORMALS, 1 ); |
Данный метод имеет два параметра: номер источника и второй – булевская переменная (истина- включение источника, ложь - выключение).
Ниже приведен пример освещения направленным источником света треугольной грани, у которой нормали в каждой вершине одинаковы. При этом положение камеры (наблюдателя) задано точкой (2,2,-2), а направление лучей света – (-2,-2,2).
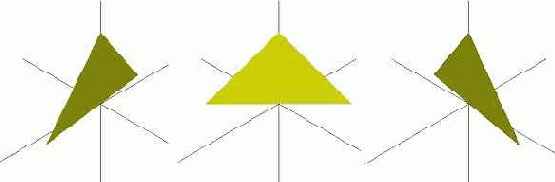
Как видно в каждом положении грань освещена одинаково (нормали в каждой вершине равны (0, 0, -1)). Изменив хотя бы одну нормаль вершины, можно добиться того, что грань будет освещаться уже неравномерно. Пусть одна из вершин будет теперь иметь нормаль (1,0,-1). Результат освещенности грани при таких изменениях нормали показан ниже.
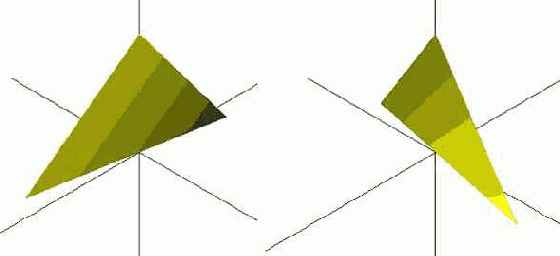
Ниже приведены примеры заполнения "нужных" полей для точечного и прожекторного источников света.
Пример для точечного источника света.
| C++ | D3DLIGHT9 light; ZeroMemory( &light, sizeof(D3DLIGHT9) ); light.Type = D3DLIGHT_POINT; light.Diffuse = D3DXCOLOR(1.0f, 0.0f, 0.0f, 0.0f); light.Position = D3DXVECTOR3(2.0f, 2.0f, -2.0f); light.Attenuation0 = 1.0f; light.Range = 100; |
| Pascal | var light: TD3DLight9; ... ZeroMemory(@light, SizeOf(TD3DLight9)); light._Type:=D3DLIGHT_POINT; light.Diffuse:=D3DXColor(1,1,0,0); light.Position:=D3DXVector3(2,2,-2); light.Attenuation0:=1; light.Range:=100; |
| C++ | D3DLIGHT9 light; ZeroMemory( &light, sizeof(D3DLIGHT9) ); light.Type = D3DLIGHT_SPOT; light.Diffuse = D3DXCOLOR(1.0f, 0.0f, 0.0f, 0.0f); light.Position = D3DXVECTOR3(2.0f, 2.0f, -2.0f); D3DXVECTOR3 direction = D3DXVECTOR3(-2.0f, -2.0f, 2.0f); D3DXVec3Normalize( (D3DXVECTOR3*)&light.Direction, &direction ); light.Attenuation0 = 1.0f; light.Range = 100; light.Phi = D3DX_PI/2; light.Theta = D3DX_PI /3; light.Falloff = 1.0f; |
| Pascal | var light: TD3DLight9; ... ZeroMemory(@light, SizeOf(TD3DLight9)); light._Type:=D3DLIGHT_SPOT; light.Diffuse:=D3DXColor(1,1,0,0); light.Position:=D3DXVector3(2,2,-2); D3DXVec3Normalize(light.Direction, D3DXVector3(-2,-2,2)); light.Attenuation0:=1; light.Range:=100; light.Phi:=pi/2; light.Theta:=pi/3; light.Falloff:=1; |
Построение стандартных объектов
Библиотека Direct3D располагает рядом встроенных функций для построения простых стандартных трехмерных примитивов (куб, цилиндр, сфера, тор):
D3DXCreatePolygon // полигонD3DXCreateBox // параллелограммD3DXCreateCylinder // цилиндрD3DXCreateSphere // сфераD3DXCreateTorus // торD3DXCreateTeapot // чайник
При создании объектов таким способом вершины "получают" формат, в котором присутствует положение (D3DFVF_XYZ) и нормаль (D3DFVF_NORMAL). Существует возможность задавать уровень детализации при создании перечисленных выше трехмерных примитивов. Следует заметить, что нормаль к каждой вершине созданного объекта вычисляется автоматически. Рассмотрим их функции создания и визуализации. Для работы с подобными примитивами необходимо объявить переменную интерфейсного типа ID3DXMesh, в которой и будет "храниться" трехмерный объект. Визуализация созданного объекта осуществляется вызовом метода DrawSubset интерфейса ID3DXMesh.
Функция создания полигона (правильного многоугольника):
D3DXCreatePolygon( ссылка на устройство вывода, длина стороны полигона, количество сторон полигона, результат, указатель на смежные треугольники);
Ниже приведен пример создания и визуализации трехмерного объекта – полигона.
| C++ |
// объявление переменной LPD3DXMESH polygon; // создание объекта полигон D3DXCreatePolygon( device, 0.5, 10, &polygon, NULL); // визуализация polygon->DrawSubset(0); |
| Pascal |
// объявление переменной var polygon: ID3DXMesh; // создание объекта полигон D3DXCreatePolygon(device, 0.5, 10, polygon, nil); // визуализация polygon.DrawSubset(0); |
Ниже приведены примеры построения полигонов с разными значениями второго и третьего параметра рассмотренной функции.
| Длина стороны = 0.5
Количество сторон = 10 | Длина стороны = 2
Количество сторон = 3 | Длина стороны = 0.1
Количество сторон = 36 | |||
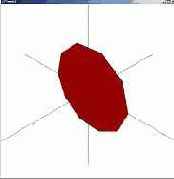 |
 |
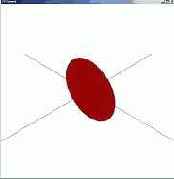 |
Функция вывода параллелепипеда
D3DXCreateBox( ссылка на устройство вывода, ширина, высота, глубина, результат, указатель на смежные треугольники);
Ниже приведен пример создания и визуализации трехмерного объекта – полигона.
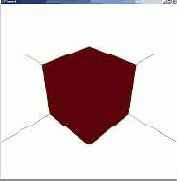
| C++ | // объявление переменной LPD3DXMESH box; // создание объекта D3DXCreateBox( device, 1.0f, 0.5f, 2.0f, &box, NULL); // визуализация box->DrawSubset(0); |
| Pascal | // объявление переменной var box: ID3DXMesh; // создание объекта D3DXCreateBox(device, 1, 0.5, 2, box, nil); // визуализация box.DrawSubset(0); |
| ширина = 1 высота = 0.5 глубина = 2 | ширина = 1 высота = 1 глубина = 1 | ширина = 0.5 высота = 2 глубина = 1 |
 |  |  |
D3DXCreateCylinder( ссылка на устройство радиус первого основания радиус второго основания высота цилиндра количество разбиений "по радиусу" количество разбиений "по длине" результат указатель на смежные треугольники);
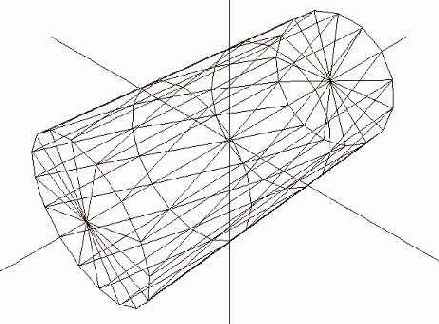
| C++ | LPD3DXMESH cylinder; D3DXCreateCylinder(device, 0.2f, 0.2f, 1, 16, 3, &cylinder, NULL); cylinder->DrawSubset(0); |
| Pascal | var cylinder: ID3DXMesh; D3DXCreateCylinder(device, 0.2, 0.2, 1, 16, 3, cylinder, nil); cylinder.DrawSubset(0); |
| Первое основание = 0.2 Второе основание = 0.2 Разбиений по радиусу = 16 | Первое основание = 0.4 Второе основание = 0.2 Разбиений по радиусу = 16 | Первое основание = 0.4 Второе основание = 0 Разбиений по радиусу = 6 |
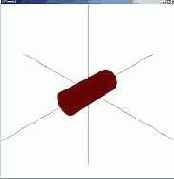 |  |  |
D3DXCreateSphere( ссылка на устройство, радиус сферы, разбиений "по радиусу", // число апельсиновых долек разбиений "вдоль", // результат, указатель на смежные треугольники);
| Разбиений по радиусу = 6, вдоль = 32 | Разбиений по радиусу = 32, вдоль = 6 |
 | 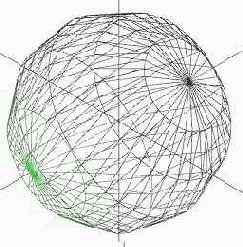 |
| C++ | LPD3DXMESH sphere; D3DXCreateSphere(device, 1.0f, 16, 16, &sphere, NULL); sphere->DrawSubset(0); |
| Pascal | var sphere: ID3DXMesh; D3DXCreateSphere(device, 1, 16, 16, sphere, nil); sphere.DrawSubset(0); |
D3DXCreateTorus( ссылка на устройство, внутренний радиус тора, внешний радиус тора, количество разбиений в поперечном сечении, количество разбиений по кругу, результат, указатель на смежные треугольники);
| Разбиений в сечение = 6 Разбиений по кругу = 32 | Разбиений в сечение = 32 Разбиений по кругу = 6 |
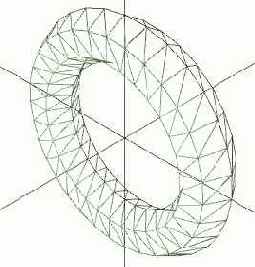 | 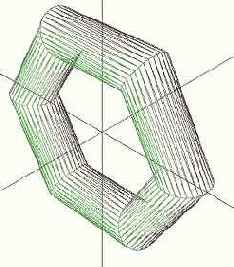 |
table class="xml_table" cellpadding="2" cellspacing="1">
LPD3DXMESH torus; D3DXCreateTorus(device, 0.2f, 0.8f, 32, 6, &torus, NULL); torus->DrawSubset(0);
var torus: ID3DXMesh; D3DXCreateTorus(device, 0.2, 0.8, 32, 6, torus, nil);
torus.DrawSubset(0);
D3DXCreateTeapot( ссылка на устройство, результат, указатель на смежные треугольники);
Это единственный примитив, для которого отсутствует возможность задать уровень детализации.
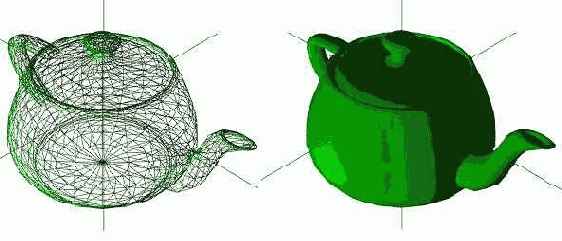
| C++ | LPD3DXMESH teapot; D3DXCreateTeapot(device, &teapot, NULL); teapot->DrawSubset(0); |
| Pascal | var teapot: ID3DXMesh; D3DXCreateTeapot(device, teapot, nil); teapot.DrawSubset(0); |
| light.Ambient = D3DXCOLOR(0.3f, 0,0,0); |  |
light.Diffuse = D3DXCOLOR(0.5f, 0.0, 0,0); light.Ambient = D3DXCOLOR(0.2f, 0,0,0); | 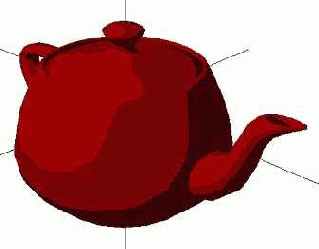 |
| light.Diffuse = D3DXCOLOR(0.5, 0.0, 0,0); light.Ambient = D3DXCOLOR(0.2, 0,0,0); light.Specular = D3DXCOLOR(0.3,0,0.0,0); | 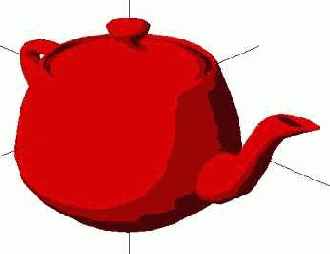 |
| C++ | device->SetRenderState( D3DRS_SPECULARENABLE, TRUE ); |
| Pascal | device.SetRenderState(D3DRS_SPECULARENABLE, 1); |
| C++ | D3DMATERIAL9 material; D3DLIGHT9 light0, light1, light2; ZeroMemory( &material, sizeof(D3DMATERIAL9) ); material.Diffuse=D3DXCOLOR(1.0f, 1.0f, 1.0f, 0.0f); ZeroMemory( &light0, sizeof(D3DLIGHT9) ); light0.Type = D3DLIGHT_POINT; light0.Diffuse = D3DXCOLOR(0.5f, 0.0f, 0.0f, 0.0f); light0.Position = D3DXVECTOR3(4.0f, 0.0f, 0.0f); … ZeroMemory( &light1, sizeof(D3DLIGHT9) ); light1.Type = D3DLIGHT_POINT; light1.Diffuse = D3DXCOLOR(0.0f, 0.5f, 0.0f, 0.0f); light1.Position = D3DXVECTOR3(0.0f, 0.0f, -4.0f); … ZeroMemory( &light2, sizeof(D3DLIGHT9) ); light2.Type = D3DLIGHT_POINT; light2.Diffuse = D3DXCOLOR(0.0f, 0.0f, 0.5f, 0.0f); light2.Position = D3DXVECTOR3(-4.0f, 0.0f, 0.0f); device->SetRenderState( D3DRS_LIGHTING, TRUE ); ... // процедура рендеринга device->SetLight( 0, &light0 ); device->LightEnable( 0, TRUE ); device->SetLight( 1, &light1 ); device->LightEnable( 1, TRUE ); device->SetLight( 2, &light2 ); device->LightEnable( 2, TRUE ); |
| Pascal | var material: TD3DMaterial9; light0, light1, light2: TD3DLight9; ZeroMemory(@material,SizeOf(TD3DMaterial9)); material.Diffuse:=D3DXColor(1,1,1,0); light0._Type:=D3DLIGHT_POINT; light0.Diffuse:=D3DXColor(0.5, 0.0, 0, 0); light0.Position:=D3DXVector3(4,0,0); … light1._Type:=D3DLIGHT_POINT; light1.Diffuse:=D3DXColor(0.0, 0.5, 0, 0); light1.Position:=D3DXVector3(0,0,-4); … light2._Type:=D3DLIGHT_POINT; light2.Diffuse:=D3DXColor(0.0, 0.0, 0.5, 0); light2.Position:=D3DXVector3(-4,0,0); … device.SetRenderState(D3DRS_LIGHTING, 1); // процедура рендеринга device.SetLight(0,light0); device.LightEnable(0,true); device.SetLight(1,light1); device.LightEnable(1,true); device.SetLight(2,light2); device.LightEnable(2,true); |

Сложные ( содержащие десятки тысяч вершин) объекты, как правило, создаются в профессиональных трехмерных редакторах (3D Studio, Maya, LightWave, и т.п.). Библиотека Direct3D содержит средства для загрузки и визуализации моделей, содержащихся в x-файлах. Х-файл – файл, содержащий в себе данные о трехмерном объекте (координаты вершин, материалы, нормали, текстуры и анимацию). Вначале необходимо объявить нужные переменные.
| C++ | LPD3DXMESH mesh; |
| Pascal | var mesh: ID3DXMesh; |
D3DXLoadMeshFromX( путь до файла на диске, набор флагов, указатель на устройство вывода, информация о смежных треугольниках, данные о материалах модели, данные об эффектах модели, количество материалов в модели, результат ).
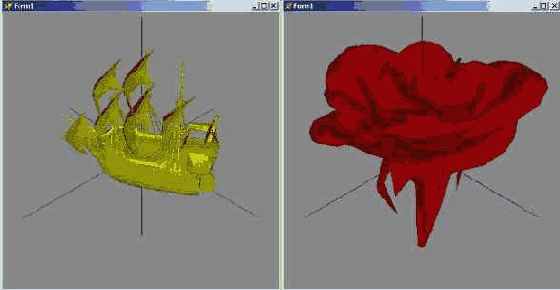
В простейшем случае (если модель не содержит информации о материалах, текстурах, смежности граней) параметры с четвертого по седьмой включительно выставляют в NULL. Ниже приведен пример загрузки модели из Х-файла.
| C++ | D3DXLoadMeshFromX("ship.x", D3DXMESH_MANAGED, device, NULL, NULL, NULL, NULL, &mesh); |
| Pascal | D3DXLoadMeshFromX('ship.x', D3DXMESH_MANAGED, device, nil, nil, nil, nil, mesh); |
| C++ | mesh->DrawSubset(0); |
| Pascal | mesh.DrawSubset(0); |
Реалистичные построения
Принцип текстурирования трехмерных объектов ничем не отличается от двумерного аналога. Для каждой треугольной грани необходимо задать текстурные координаты. Единственное отличие от двумерного варианта заключается в формате вершин и наборе FVF флагов.
| C++ |
struct VERTEX3D { FLOAT x, y, z; FLOAT u, v; }; #define MY_FVF (D3DFVF_XYZ | D3DFVF_TEX1); ... VERTEX3D points[3] = { { -1.0f,-1.0f, 0.0f, 0.0f, 1.0f, }, { 0.0f, 1.0f, 0.0f, 0.5f, 0.0f, }, { 1.0f,-1.0f, 0.0f, 1.0f, 1.0f, } } |
| Pascal |
type Vertex3D = packed record x, y, z: Single; u, v: Single; end; const MY_FVF = D3DFVF_XYZ or D3DFVF_TEX1; var points: array [0..2] of Vertex3D = ( (x: -1; y: -1; z: 0; u: 0; v: 1), (x: 0; y: 1; z: 0; u: 0.5; v: 0), (x: 1; y: -1; z: 0; u: 1; v: 1) ); |
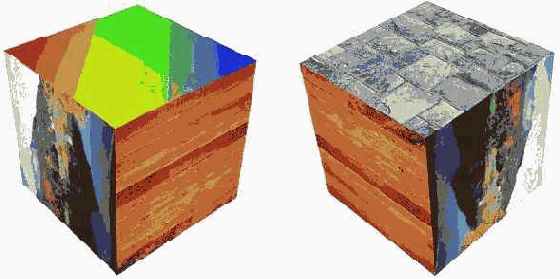
Ниже показан пример вывода куба, у которого все грани покрыты различными текстурами. Для этого можно объявить массив для хранения текстур из шести элементов типа IDirect3DTexture9.
| C++ |
LPDIRECT3DTEXTURE9 textures[6]; LPCSTR files[] = { {"bricks.bmp"}, {"colors.bmp"}, {"Lake.bmp"}, {"stone_wall.bmp"}, {"wall.bmp"}, {"fur.jpg"} }; ... for (int i=0; i<6; i++) D3DXCreateTextureFromFile( device, files[i], &textures[i] ); |
| Pascal |
var textures: array [0..5] of IDirect3DTexture9; files: array [0..5] of AnsiString = ( ('bricks.bmp'), ('colors.bmp'), ('Lake.bmp'), ('stone_wall.bmp'), ('wall.bmp'), ('fur.jpg') ); ... for i:=0 to 5 do D3DXCreateTextureFromFile(device, PChar(files[i]), textures[i]); |
Теперь если куб у нас храниться в виде 12 независимых треугольных граней, то его вывод может быть осуществлен с помощью следующего кода.
| C++ |
for (int i=0; i<6; i++) { device->SetTexture(0, &textures[i]); device->DrawPrimitive(D3DPT_TRIANGLELIST, i*6, 2); } |
| Pascal |
for i:=0 to 5 do begin device.SetTexture(0, textures[i]); device.DrawPrimitive(D3DPT_TRIANGLELIST, i*6, 2); end; |
Ниже приведены примеры (кадры анимации) вращения такого куба.
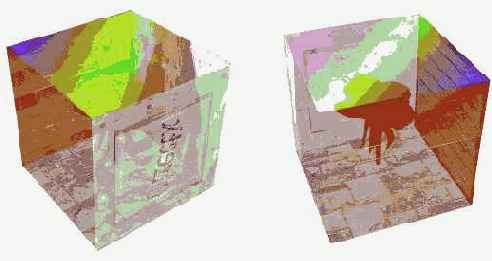
Рассмотрим один из способов построения полупрозрачных трехмерных объектов.
Данный метод прозрачности применим только для выпуклых объектов. Идея его заключается в следующем. Вначале выводятся те грани объекта, которые считаются невидимыми для наблюдателя (задние грани). Затем включается режим полупрозрачности (смешивания цветов). Выводим грани объекта, которые видны наблюдателю. Отображение "передних" и "задних" для наблюдателя сторон объекта можно осуществить с помощью механизма отсечения граней. Предположим, что вершины грани перечислены по часовой стрелке. Тогда отключение вывода таких граней отобразит нам "задние" стороны примитива (в нашем случае куба). Программно этот шаг может выглядеть так.
| C++ | device->SetRenderState( D3DRS_CULLMODE, D3DCULL_CW ); for (int i=0; i<6; i++) { device->SetTexture(0, &textures[i]); device->DrawPrimitive(D3DPT_TRIANGLELIST, i*6, 2); } |
| Pascal | device.SetRenderState(D3DRS_CULLMODE, D3DCULL_CW); for i:=0 to 5 do begin device.SetTexture(0,textures[i]); device.DrawPrimitive(D3DPT_TRIANGLELIST, i*6, 2); end; |

Включение полупрозрачности с нужными параметрами смешивания цветов.
| C++ | device->SetRenderState( D3DRS_ALPHABLENDENABLE, TRUE ); device->SetRenderState( D3DRS_SRCBLEND, D3DBLEND_SRCCOLOR ); device->SetRenderState( D3DRS_DESTBLEND, D3DBLEND_INVSRCCOLOR ); |
| Pascal | device.SetRenderState(D3DRS_ALPHABLENDENABLE, 1); device.SetRenderState(D3DRS_SRCBLEND, D3DBLEND_SRCCOLOR); device.SetRenderState(D3DRS_DESTBLEND, D3DBLEND_INVSRCCOLOR); |
| C++ | device->SetRenderState( D3DRS_CULLMODE, D3DCULL_CCW ); for (int i=0; i<6; i++) { device->SetTexture(0, &textures[i]); device->DrawPrimitive(D3DPT_TRIANGLELIST, i*6, 2); } |
| Pascal | device.SetRenderState(D3DRS_CULLMODE, D3DCULL_CCW); for i:=0 to 5 do begin device.SetTexture(0,textures[i]); device.DrawPrimitive(D3DPT_TRIANGLELIST, i*6, 2); end; |
Для придания трехмерной сцене еще большей реалистичности можно добавить тени, которые отбрасывают объекты при освещении их некоторым источником света. Алгоритмы затенения в случае точечных источников света схожи с алгоритмами удаления невидимых поверхностей, с единственным лишь отличием. В алгоритмах удаления невидимых граней определяются поверхности, которые можно увидеть из точки положения наблюдателя, а в алгоритмах затенения выделяются поверхности, которые можно "увидеть" из местоположения источника света. Грани, видимые как из точки наблюдения, так и из источника света, не лежат в тени. Те же поверхности, которые видимы из точки наблюдения, но не видимы из источника света, находятся в тени.
Рассмотрим один из простейших и очень быстрых алгоритмов построения теней. Он предназначен для просчета резких теневых участков от полигональных объектов на ровную поверхность (плоскость). Конечно, этот алгоритм очень ограничен в возможностях, но в то же время он прост для реализации. Основная идея метода заключается в том, что для каждого полигона (треугольной грани) сцены, создается еще один полигон, который будет представлять собой тень первого. Все вершины тени будут находиться в пределах плоскости, на которую производится проекция. Алгоритм построения тени будет содержать следующие шаги:
Создать луч, начинающийся в источнике света, проходящий через вершину полигона и пересекающий плоскость проецирования;Получить (найти) точку пересечения этого луча с плоскостью;Проделать шаги 1 и 2 для всех вершин грани, получив таким образом координаты "теневого" полигона и затем отрисовать его обычными методами.
Пусть у нас источник света находится в точке L=(Lx,Ly,Lz), треугольная грань объекта имеет координаты вершин P=(Px,Py,Pz), Q=(Qx,Qy,Qz), R=(Rx,Ry,Rz), а плоскость проецирования (затенения)




С другой стороны точка M лежит в плоскости

Подставим выражения для Mx,My,Mz в уравнение плоскости: A*(Lx+t(Px-Lx))+B*(Ly+t(Py-Ly))+C*(Lz+t(Pz-Lz))+D=0. Это линейное уравнение относительно параметра t, решая которое находим, что



Аналогичные шаги проделываем для двух других вершин полигона Q и R. Следует заметить, что при вычислении тени на плоскость y=0, параметр

Рассмотренный метод имеет несколько "подводных камней". Тень будет прорисовываться даже в том случае, если источник света находится между полигоном и плоскостью проецирования или же источник света расположен вообще по другую сторону от плоскости. Поэтому такие ситуации необходимо отслеживать и корректно обрабатывать.
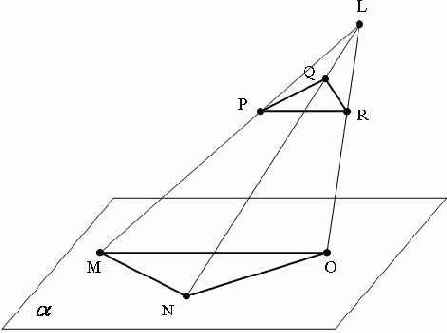
Ниже приводится пример отбрасывания тени от трехмерного объекта (птицы) на плоскость, покрытую текстурой. В одном случае "тень" является непрозрачной, а в другом – прозрачной.

Рассмотрим способ построения ландшафтов и поверхностей средствами библиотеки Direct3D. Данная задача сводится к тому, чтобы на регулярной сетке из треугольников построить трехмерную поверхность (график функции двух переменных, земная поверхность, и т.п.).

Разберем построение трехмерной поверхности, представляющей собой функцию двух переменных y=f(x,z). Пусть для простоты у нас область определения функции f(x,z) ограничена единичным квадратом, т.е. 0<=x<=1, 0<=z<=1. Визуализация рассмотренных поверхностей на растровых устройствах может быть осуществлена путем кусочно-линейной аппроксимации треугольными гранями. Такая триангуляционная поверхность может быть получена следующим образом. Параметрическое пространство x,z (единичный квадрат) дискретизируется по координате x с шагом dx, по координате z – с шагом dz. Для каждой пары значений (x,z) вычисляется точка на поверхности y=f(x,z). Полученный таким образом массив точек триангулируется регулярной сеткой.
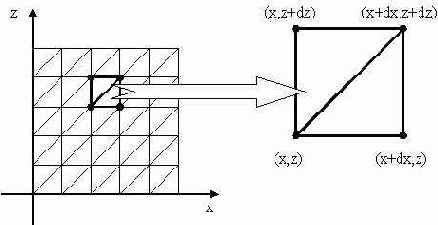
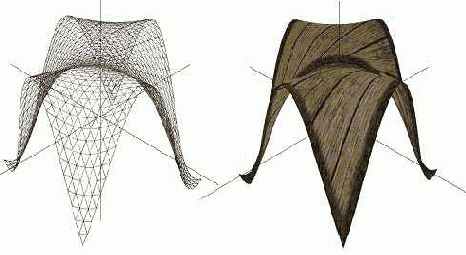
Ниже приведены два примера построения трехмерных поверхностей (график функции двух переменных и элементарная поверхность Безье третьей степени) , причем на обе поверхности наложены текстуры.

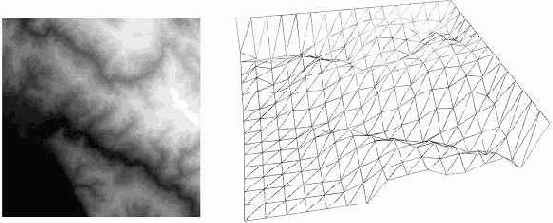
Разберем один из способов построения ландшафтов, который базируется на так называемой карте высот. Карта высот представляет собой двумерный массив, где каждый элемент (пиксель) определяет высоту точки в сетке треугольников. Как правило, значение высоты ранжируется в диапазоне от 0 до 255. Поэтому для хранения подобных карт высот используют изображения в оттенках серого цвета (grayscale image). Более светлые участки на таких изображениях соответствуют более высоким значениям точек, а темные участки определяют низкие значения высот. Кроме этого подбирается текстура, схожая по "характеру" с ландшафтом. Ниже приведен пример построения ландшафта по карте высот.

Графический процессор в задачах обработки изображений
Проблема большого количества вычислений возникает в ряде задач многих направлений науки и техники. На сегодняшний день, когда с помощью компьютеров решаются, чуть ли не все задачи человечества, применение электронных вычислительных машин является естественно разумным шагом. Среди всего множества задач можно выделить некоторый спектр, для решения которых требуется от нескольких часов до нескольких дней машинного времени. Среди таких ресурсоемких в вычислительном плане задач и направлений можно отметить следующие: предсказание погоды, климата и глобальных изменений в атмосфере, генетика человека, астрономия, транспортные задачи, гидро- и газодинамика, управляемый термоядерный синтез, разведка нефти и газа, вычислительные задачи наук о мировом океане, распознавание изображений и синтез речи. Использование суперкомпьютеров с большим количеством независимо работающих параллельных процессоров и технологий высокопроизводительных вычислений может существенно снизить заявленные выше временные оценки. Такой подход
является заведомо очень дорогим в финансовом плане и позволителен для узкого круга исследователей и ученых. Тем не менее, сейчас в области настольных персональных компьютеров начинают широко распространяться процессоры с несколькими независимыми ядрами, что позволяет решать уже некоторые задачи в параллельном режиме более широкому кругу обычных пользователей и специалистов. Однако количество ядер в таких процессорах ограничено, как правило, двумя либо четырьмя штуками, что не всегда дает особого приращения производительности. Но современный персональный компьютер в большинстве случаев может быть оснащен сегодня помимо мощного центрального процессора (CPU - Central Processing Unit) еще и современной видеокартой с графическим процессором (GPU - Graphics Processing Unit) производительностью несколько сотен миллиардов операций с плавающей точкой в секунду. Даже самые современные серверные процессоры далеки от такой производительности. Вообще изначально область применения графического пр оцессора была просчет и отображение трехмерных сцен.
Однако, с появлением видеокарт, позволяющих их программировать, круг вычислительных задач, решаемых с помощью графического процессора, существенно расширился. Поэтому возникает резонный вопрос. Почему бы не задействовать вычислительные ресурсы графического процессора для решения задач отличных от его "традиционных" графических? Как мы уже уяснили, обработка вершин и пикселей в графическом конвейере ведется в параллельном режиме. Количество параллельных блоков по преобразованию вершин зависит от модели графического процессора и может колебаться от 2 до 8 штук. Аналогично блок пиксельной обработки также функционирует в параллельном режиме, причем количество пиксельных блоков может быть от 4 до 48 штук в зависимости от типа видеокарты (на момент написания данных строк).
В качестве области исследования и проведения вычислительных экспериментов рассмотрим точечные процессы цифровой обработки изображений. С цифровой обработкой изображений сталкиваются при решении многих научных и технических задач. Обработка изображений в широком смысле слова означает выполнение различных операций над многомерными сигналами, которыми изображения и являются. Цели, преследуемые при обработке изображений весьма различны и, как правило, зависят от конкретной решаемой задачи. Это может быть улучшение яркости или контраста в вашей домашней коллекции цифровых фотографий, получение монохромных (бинарных) изображений, обработка изображений сглаживающими фильтрами для удаления шумов и мелких искажений, выделение значимых признаков на изображении с применением в последствии алгоритмов распознавания, например, формы символов. Современная жизнь ставит ряд требований к подобным методам обработки. Одно из самых главных это высокая эффективность и скорость работы алгоритмов с использованием персонального
ФЄ компьютера. Традиционно обработкой изображений занимался центральный процессор системы. Для этого каждый элемент изображения (пиксель) подвергался некоторому, как правило, однотипному преобразованию.
И в результате получалось, что для изображения размерами M на N пикселей требуется MxN операций процессора. При значительных размерах изображения этот объем вычислений может оказаться критическим для одного устройства обработки информации. Поэтому, чтобы снизить вычислительную нагрузку алгоритма вполне резонно воспользоваться идеями и методами параллельных вычислений. Однако привлечение дорогостоящих параллельных суперкомпьютеров в данной задаче не является критически необходимым. Подобный класс задач можно попытаться решить с помощью обычной современной видеокарты, стоимость которой на несколько порядков меньше любого вычислительного кластера. Под точечными процессами будем понимать набор алгоритмов, которые подвергают обработке каждый пиксель изображения независимо от оста льных элементов. Примерами точечных пр оцессов могут выступать: приведение цветного изображения к оттенкам серого цвета, увеличение/уменьшение яркости и контраста, негативное преобразование, пороговое отсечение, соляризация и др. Следует отметить, что перечисленные точечные процессы мы будем рассматривать для изображений в оттенках серого цвета, так называемых grayscale. В подобных изображениях присутствуют только 256 оттенков какого-либо основного цвета. Как правило, используются оттенки серого цвета так, что палитра цветов содержит 256 "плавноизменяющихся" от черного к белому цвету интенсивностей. При этом черный цвет кодируется нулем, белый – числом 255. Таким образом, точечный процесс можно представить как некую функцию, определенную на целочисленном дискретном множестве [0…255] с таким же множеством значений.
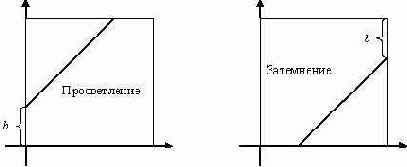
Преобразование просветления увеличивает или уменьшает значение яркости каждого пикселя в отдельности. Пусть I(x,y) – значение яркости пикселя (x,y) в изображении I. Тогда операция просветления на языке формул может быть выражена следующим образом: I(x,y)= I(x,y)+b, где b – постоянная яркости. Если b>0, то яркость в изображении будет увеличиваться (просветление); если же b<0, то яркость будет уменьшаться (затемнение).
Могут возникнуть случаи, при которых значение выражения I(x,y)+b выйдет за пределы отрезка [0…255]. В этом случае значение, вышедшее за границы отрезка приводят к значению ближайшей границы, т.е. либо к 0, либо к 255. Графически операцию просветления можно описать следующими графиками функций.
Рассмотрим произвольное изображение I в оттенках серого цвета. Введем массив H, содержащий 256 элементов: H[0…255]. Каждый i-й элемент этого массива будет содержать количество пикселей в изображении I со значением интенсивности i. Если визуализировать массив H в виде графика функции, то получим так называемую гистограмму интенсивностей яркости исходного изображения I. Вид гистограммы позволяет получить представление об общей яркости изображения. Гистограмма интенсивности является информативным инструментом при анализе общей яркости в изображении. Способ получения гистограммы интенсивности изображения можно записать на алгоритмическом языке следующим образом.
Цикл по x от 0 до ШиринаИзображения-1 Цикл по y от 0 до ВысотаИзображения-1 ТелоЦикла k = I(x,y); H[k] = H[k] + 1; КонецТелоЦикла
Ниже на рисунке приведены три гистограммы интенсивности различного класса.
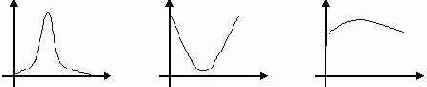
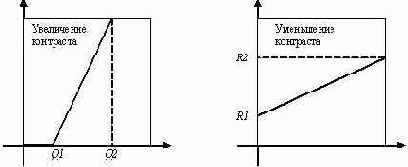
Гистограмма слева определяет изображения, в которых мало пикселей черного и белого цветов (низкоконтрастные изображения). Гистограмма посередине соответствует изображениям, в которых число черных и белых пикселей значительно превышает все остальные (высококонтрастные изображения). И гистограмма справа представляет изображения, в которых количество пикселей с различными интенсивностями цветов приблизительно одинаково (нормальноконтрастные изображения). Изменение контраста в изображении можно осуществить с помощью линейных преобразований. Для гистограмм, соответствующих низкоконтрастным изображениям, выделяют отрезок [Q1,Q2], на котором сосредоточена значительная часть интенсивностей. Затем данный отрезок [Q1,Q2] линейно отражают в отрезок [0…255] с помощью следующего преобразования: I(x,y)= 255*(I(x,y)-Q1)/(Q2-Q1). Аналогично можно получить формулу для уменьшения контраста в изображении.
В этом случае преобразование будет иметь следующий вид: I(x,y)= R1+I(x,y)*(R2-R1)/255, где [R1,R2] – некий отрезок, в который отображается все множество значений интенсивностей. Графически операции увеличения и уменьшения контрастности в изображении можно представить следующим образом.
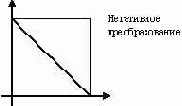
Негативное преобразование инвертирует значения интенсивностей яркости так, что темные пиксели становятся светлыми и наоборот. Математически это задается довольно простой формулой:
I(x,y)= 255- I(x,y), а графически это выглядит следующим образом.
Пороговое отсечение (бинаризация) преобразует изображение в оттенках серого в изображение, в котором присутствует всего два цвета, как правило, белый и черный (бинарное). На языке формул бинаризация имеет такой вид: I(x,y)=0, если I(x,y)>p; I(x,y)=255, если I(x,y)<p, где p – некоторый заданный порог. Графически операция порогового отсечения задается следующим образом.
Очень часто пороговое отсечение применяется как промежуточный шаг в задачах распознавания изображений для устранения ошибок сканирования и оцифровки.
Получение изображения в оттенках серого из цветного также можно отнести к точечным процессам. Каждый пиксель цветного изображения представляет собой тройку байт, значения которых соответствуют весам красного, зеленого и синего цветов. Это так называемая цветовая модель RGB (Red, Green, Blue). Преобразование цветного изображения в оттенки серого осуществляется по следующей формуле:
I=0.3*R+0.59*G+0.11*B, где I – значение интенсивности серого цвета, R, G, B - значения весов красного, зеленого и синего цветов соответственно.
Ниже представлены результаты обработки исходного изображения пиксельным шейдером.
sampler tex0;
struct PS_INPUT { float2 base : TEXCOORD0; }; struct PS_OUTPUT { float4 diffuse : COLOR0; }; PS_OUTPUT Main (PS_INPUT input) { PS_OUTPUT output; float4 col = tex2D(tex0, input.base); ... return output; };
| Исходное изображение |  |
| Приведение к оттенкам серого цвета float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); output.diffuse = dot(lum,col); |  |
| Увеличение яркости float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); output.diffuse = dot(lum,col)+0.2f; |  |
| Уменьшение яркости float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); output.diffuse = dot(lum,col)-0.2f; |  |
| Увеличение контраста float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); float gray = dot(lum,col); float Q1 = 0.2f; float Q2 = 0.7f; if (gray > Q2) gray = 1.0f; else if (gray < Q1) gray = 0.0f; else gray = (gray - Q1)/(Q2-Q1); output.diffuse = gray; |  |
| Уменьшение контраста float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); float gray = dot(lum,col); float R1 = 0.2f; float R2 = 0.7f; gray = R1+gray*(R2-R1); output.diffuse = gray; |  |
| Пороговое отсечение (бинаризация) float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); float gray = dot(lum,col); float p = 0.4f; if (gray > p) gray = 1.0f; else if (gray < p) gray = 0.0f; output.diffuse = gray; |  |
| Негативное преобразование float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); float gray = dot(lum,col); output.diffuse = 1.0f-gray; |  |
Рассмотрим теперь некоторые методы обработки изображения с использованием пространственных процессов. В этом случае элемент изображения получает новое значение на основе группы элементов, примыкающих к данному. Область (окрестность) примыкания представляет собой группу элементов изображения использующаяся в пространственных процессах. Как правило, область примыкания есть квадратная матрица нечетной размерности с центром в обрабатываемом элементе.

Пространственная частота изображения – скорость изменения яркости по координатам. Говорят, что присутствует высокая частота в изображении, если яркость меняется очень сильно. Одной из центральных задач в обработке изображений является построение пространственного фильтра. Фильтр позволяет усилить или ослабить компоненты различной частоты. Пространственный фильтр – процесс, который способен выделить (подчеркнуть) компоненты определенной частоты. Двумерный фильтр устроен следующим образом. Берется матрица размером 3х3, 5х5, 7х7 и т.д. и на ней определяется некоторая функция Упомянутая матрица называется окном или апертурой, а заданная на нем функция – весовой или функцией окна. Каждому элементу окна соответствует число, называемое весовым множителем. Совокупность всех весовых множителей и составляет весовую функцию. Нечетные размеры апертуры объясняются однозначностью определения центрального элемента. Фильтрация осуществляется перемещением окна (апертуры) фильтра по изображению. В каждом положении апертур
ФЄ ы выполняются однотипные действия, которые определяют так называемый отклик фильтра. Весовая функция в процессе перемещения остается неизменной. В каждом положении окна происходит операция свертки – линейная комбинация значений элементов изображения:




Низкочастотный фильтр – процесс, который ослабляет высокочастотные компоненты и усиливает роль низкочастотных.
Сглаживание изображения реализуется с помощью следующих ядер.

Следует заметить, что общая яркость исходного изображения и результирующего будет одинаковой.
Фильтры высокой частоты применяются для выделения таких деталей, как контуры, границы или для повышения резкости изображения. Каждый скачок яркости и каждый контур представляют собой интенсивные детали, связанные с повышенными частотами. С помощью высокочастотного фильтра можно так видоизменить изображение, чтобы скачки яркости на контурах будут сильно подчеркнуты, а в предельном случае вообще останутся только контуры. Ниже приведены примеры ядер высокочастотных фильтров.

Медианный фильтр – пространственный процесс, который не подпадает под категорию свертки. Усредненное фильтрование использует значения элементов, содержащихся в области примыкания, для определения нового значения. Фильтр располагает элементы области примыкания в возрастающем порядке и отбирает среднее значение.

Результатом усредненного фильтра является то, что любой случайный шум, содержащийся в изображении, будет устранен. Это происходит потому, что любое случайное резкое изменение интенсивности элемента в пределах области примыкания, будет сортироваться, т.е. будет помещено либо в начало, либо в конец отсортированного списка.
Другим пространственным процессом, который можно продемонстрировать, используя свертку, является усиление края. В отличие от задачи обострения контуров (высокочастотный фильтр) здесь основной целью является не улучшение изображения, а наоборот, контуры должны быть отделены от всего изображения так, чтобы выходное изображение состояло только из контуров. Рассмотрим основные методы усиления края.
Метод усиления края по Лапласу не зависит от направления краев, и высвечиваются все направления. Ниже приведены три лапласиана.

Метод усиления края с помощью оператора Собеля рассматривает два различных ядра свертки:

Исходя из этих сверток, вычисляется величина и направление краев.
В качестве отклика данного фильтра выступает величина



Метод усиления края с помощью оператора Превита также использует два ядра:

Результат работы оператора Превита есть max{P,Q}, где P и Q - отклики ядер


Метод преобразования реализующий эффект тиснения на изображении. Результирующее изображение выглядит как будто "выдавленным" или "вдавленным". Фильтр такого преобразования имеет вид:

Как нам известно, обращение к элементам текстуры в пиксельном шейдере производится с помощью текстурных координат. Левый верхний тексель имеет текстурные координаты (0,0), левый нижний – координаты (0,1), правый верхний – координаты (1,0), правый нижний – координаты (1,1)

Задача состоит в том, чтобы для произвольного текселя изображения, имеющего текстурные координаты (u,v), определить значения текстурных координат восьми его соседей. Пусть у нас количество текселей в каждой строке будет W, а количество текселей в каждом столбце – H. В силу того, что тексели расположены равномерно (на одинаковом расстоянии друг от друга), можно вычислить шаг приращения du и dv в текстурных координатах по горизонтали и вертикали соответственно. Итак,



Ниже приведен пример пиксельного шейдера, который реализует метод усиления границ на изображении с помощью оператора Собеля и метод тиснения, а также примеры изображений.
sampler tex0;
struct PS_INPUT { float2 base : TEXCOORD0; };
struct PS_OUTPUT { float4 diffuse : COLOR0; };
PS_OUTPUT Main (PS_INPUT input) { PS_OUTPUT output; const float W =320.0f; const float H =240.0f; const float du=1.0f/(W-1); const float dv=1.0f/(H-1); const float2 c[9] = { float2(-du, -dv), float2(0.0f, -dv), float2(du, -dv), float2(-du, 0.0f), float2(0.0f, 0.0f), float2(du, 0.0f), float2(-du, dv), float2(0.0f, dv), float2(du, dv) };
float3 col[9]; for (int i=0; i<9; i++) { col[i] = tex2D(tex0, input.base+c[i]); }
float lum[9]; float3 gray = (0.30f, 0.59f, 0.11f) ; for (int i=0; i<9; i++) { lum[i] = dot(col[i], gray); }
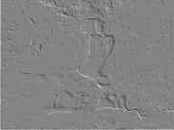
float res1 = 0.0f; float res2 = 0.0f; const float sobel1[9] = { 1, 2, 1, 0, 0, 0, -1, -2, -1}; const float sobel2[9] = {-1, 0, 1, -2, 0, 2, -1, 0, 1}; const float tisnenie[9] = {0, 1, 0, -1, 0, 1, 0, -1, 0}; for (int i=0; i<9; i++) { res1+=lum[i]*sobel1[i]; res2+=lum[i]*sobel2[i]; res+=lum[i]*tisnenie[i]; } output.diffuse = sqrt(res1*res1+res2*res2); //output.diffuse = res+0.5f; return output; };
Пример 6.1.
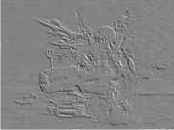
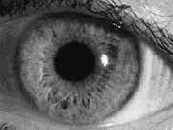
| Исходное изображение | Оператор Собеля | Метод тиснения |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |

Использование шейдеров с помощью языка HLSL
До появления на свет восьмой версии библиотеки DirectX графический конвейер представлял собой некую модель "черного ящика", когда программист мог загружать в него исходные графические данные и настраивать фиксированное количество параметров (состояний). Такой фиксированный подход связывал руки разработчикам в реализации различных спецэффектов при программировании трехмерной графики. Данный недостаток был преодолен с появлением восьмой версии графической библиотеки DirectX. Основным нововведением в ней стало появление программируемых элементов графического конвейера. Были введены так называемые вершинные шейдеры для замены блока трансформации вершин и расчета освещенности, и пиксельные шейдеры для замены блока мультитекстурирования. Теперь программист мог сам задавать правила (законы) преобразования вершин трехмерной модели в вершинном шейдере и определять способы смешивания цвета пикселя и текстурных цветов. Таким образом вершинный шейдер представляет собой небольшую п рограмму (набор инструкци й), которая оперирует с вершинными атрибутами трехмерного объекта. Пиксельный шейдер предназначен для обработки элементарных фрагментов (пикселей). Ниже представлена схема графического конвейера, где показано какой этап обработки вершин заменяется вершинными шейдерами.

Изначально шейдеры писались на языке программирования, близкого к ассемблеру. С выходом девятой версии библиотеки DirectX появилась возможность создавать (программировать) шейдеры с использованием высокоуровневого языка программирования HLSL (High-Level Shader Language), разработанного компанией Microsoft. Преимущества высокоуровневого языка программирования перед низкоуровневым очевидны:
Написание программ (кодирование) занимает меньше времени (можно посветить больше времени разработке алгоритма)Программы на языке HLSL более читабельны и удобнее в отладке.Компилятор HLSL создает более оптимизированный код чем программист.Возможность компилировать программу под любую версию шейдеров.
Рассмотрим сначала основные шаги использования вершинных шейдеров в библиотеке Direct3D с использованием языка HLSL.
Вообще говоря, вершинные шейдеры могут эмулироваться программным способом. Это означает, что вся обработка (обсчет) вершин будет производиться с помощью центрального процессора (CPU) компьютера. Программно это достигается путем указания в четвертом параметре функции создания устройства вывода, флага D3DCREATE_SOFTWARE_VERTEXPROCESSING. В случае если возможности видеокарты позволяют использование шейдеров, то указывается константа D3DCREATE_HARDWARE_VERTEXPROCESSING.
Первым шагом при работе в вершинными шейдерами необходимо задать формат вершины. Теперь это проделывается не через набор FVF флагов, а с помощью структуры D3DVertexElement9. Нужно заполнить массив типа D3DVertexElement9, каждый элемент которого представляет структуру, состоящую из шести полей. Первое поле указывает номер потока вершин, и как правило, здесь передается ноль, если используется один поток. Второе поле задает для атрибута вершины смещение в байтах от начала структуры. Так, например, если вершина имеет атрибуты позиции и нормали, то смещение для первого из них (позиции) будет 0, а для второго (нормаль) – 12, т.к. объем памяти для первого атрибута есть 3*4=12 байт. Третье поле определяет тип данных для каждого атрибута вершины. Наиболее часто используемые приведены ниже:
D3DDECLTYPE_FLOAT1 D3DDECLTYPE_FLOAT2 D3DDECLTYPE_FLOAT3 D3DDECLTYPE_FLOAT4 D3DDECLTYPE_D3DCOLOR.
Четвертое поле задает метод тесселяции (разбиения сложной трехмерной поверхности на треугольники). Здесь, как правило, передают константу D3DDECLMETHOD_DEFAULT. Пятое поле указывает на то, в качестве какого компонента планируется использовать данный вершинный атрибут. Наиболее используемые константы представлены ниже:
D3DDECLUSAGE_POSITION, D3DDECLUSAGE_NORMAL, D3DDECLUSAGE_TEXCOORD, D3DDECLUSAGE_COLOR.
И последнее, шестое поле определяет индекс для одинаковых типов вершинных атрибутов. Например, если имеется три вершинных атрибута, описанные как D3DDECLUSAGE_NORMAL, то для первого из них нужно задать индекс 0, для второго – 1, для третьего – 2.
Ниже приведен пример описания вершины, содержащей положение и цвет с помощью массива элементов D3DVertexElement9.
| C++ | D3DVERTEXELEMENT9 declaration[] = { { 0, 0, D3DDECLTYPE_FLOAT3, D3DDECLMETHOD_DEFAULT, D3DDECLUSAGE_POSITION, 0 }, { 0, 12, D3DDECLTYPE_D3DCOLOR, D3DDECLMETHOD_DEFAULT, D3DDECLUSAGE_COLOR, 0 }, D3DDECL_END() }; |
| Pascal | declaration: array [0..2] of TD3DVertexElement9 = ( (Stream: 0; Offset: 0; _Type: D3DDECLTYPE_FLOAT3; Method: D3DDECLMETHOD_DEFAULT; Usage: D3DDECLUSAGE_POSITION; UsageIndex: 0), (Stream: 0; Offset: 12; _Type: D3DDECLTYPE_D3DCOLOR; Method: D3DDECLMETHOD_DEFAULT; Usage: D3DDECLUSAGE_COLOR; UsageIndex: 0), (Stream: $FF; Offset: 0; _Type: D3DDECLTYPE_UNUSED; Method: TD3DDeclMethod(0); Usage: TD3DDeclUsage(0); UsageIndex: 0) ); |
| C++ | LPDIRECT3DVERTEXDECLARATION9 VertexDeclaration = NULL; device->CreateVertexDeclaration( declaration, &VertexDeclaration ); |
| Pascal | var VertexDeclaration: IDirect3DVertexDeclaration9; ... device.CreateVertexDeclaration( @declaration, VertexDeclaration ); |
| C++ | device->SetVertexDeclaration( VertexDeclaration ); |
| Pascal | device.SetVertexDeclaration(VertexDeclaration); |
Первый параметр функции задает строку, в которой содержится имя файла вершинного шейдера.
Второй и третий параметры являются специфическими и, как правило, здесь передаются значения NULL.
Четвертый параметр – строка, определяющая название функции в шейдере или так называемая точка входа в программу.
Пятый параметр – строка, задающая версию шейдера. Для вершинных шейдеров указывают одну из следующих строковых констант: vs_1_1, vs_2_0, vs_3_0. Шестой параметр определяет набор флагов. Здесь могут быть переданы следующие константы:
D3DXSHADER_DEBUG – указание компилятору выдавать отладочную информацию;
D3DXSHADER_SKIPVALIDATION – указание компилятору не производить проверку кода шейдера на наличие ошибок;
D3DXSHADER_SKIPOPTIMIZATION – указание компилятору не производить оптимизацию кода шейдера. Можно указать значение ноль.
Седьмой параметр – переменная, типа ID3DXBuffer, которая содержит указатель на откомпилированный код шейдера.
Восьмой параметр – переменная, содержащая указатель на буфер ошибок и сообщений.
И последний, девятый параметр – переменная типа ID3DXConstantTable, в которую записывается указатель на таблицу констант. Через данный указатель производится "общение" с константами в шейдере.
Ниже приведен пример компиляции вершинного шейдера, хранящегося в файле vertex.vsh.
| C++ | LPD3DXBUFFER Code = NULL; LPD3DXBUFFER BufferErrors = NULL; LPD3DXCONSTANTTABLE ConstantTable = NULL; ... D3DXCompileShaderFromFile( "vertex.vsh", NULL, NULL, "main", "vs_1_1", 0, &Code, &BufferErrors, &ConstantTable ); |
| Pascal | var Code: ID3DXBuffer; BufferErrors: ID3DXBuffer; ConstantTable: ID3DXConstantTable; ... D3DXCompileShaderFromFile('vertex.vsh', nil, nil, 'main', 'vs_1_1', 0, @Code, @BufferErrors, @ConstantTable); |
| C++ | LPD3DXBUFFER Code = NULL; LPDIRECT3DVERTEXSHADER9 VertexShader = NULL; ... device->CreateVertexShader( (DWORD*)Code->GetBufferPointer(), &VertexShader ); |
| Pascal | var Code: ID3DXBuffer; VertexShader: IDirect3DVertexShader9; ... device.CreateVertexShader(Code.GetBufferPointer, VertexShader); |
И заключительный шаг – установка вершинного шейдера, реализуемая через вызов метода SetVertexShader() интерфейса IDirect3DDevice9. Как правило, данный метод вызывается в процедуре вывода сцены (Render).
| C++ | LPDIRECT3DVERTEXSHADER9 VertexShader = NULL; ... device->SetVertexShader( VertexShader ); |
| Pascal | var VertexShader: IDirect3DVertexShader9; ... device.SetVertexShader(VertexShader); |
Секция глобальных переменных и константСекция, описывающая входные данные вершиныСекция, описывающая выходные данные вершиныГлавная процедура в шейдере (точка входа)
В секции глобальных переменных и констант описываются данные, которые не содержатся в вершинных атрибутах: матрицы преобразований, положения источников света и др. Ниже приведен пример описания глобальной матрицы и статичной переменной.
float4x4 WorldViewProj; static float4 col = {1.0f, 1.0f, 0.0f, 1.0f};
В секции, описывающей входные данные, определяется входная структура вершинных атрибутов. Например, для вершин, которые содержат позицию и цвет эта структура может выглядеть так.
struct VS_INPUT { float4 position : POSITION; float4 color0 : COLOR0; };
Аналогично определяется выходная структура данных шейдера.
struct VS_OUTPUT { float4 position : POSITION; float4 color0 : COLOR0; };
Используемые здесь семантические конструкции (POSITION и COLOR0) указывают на принадлежность того или иного атрибута вершины.
Так же как и в программах на языке C++, программа на языке HLSL должна иметь точку входа (главную процедуру). Здесь точка входа может быть описана следующим образом.
VS_OUTPUT main( VS_INPUT IN ) { VS_OUTPUT OUT; … return OUT; }
Вообще говоря, использование входных и выходных структур не является обязательным в языке HLSL. Можно использовать привычный для любого программиста подход передачи параметров без структур.
float4 main(in float2 tex0 : TEXCOORD0, in float2 tex1 : TEXCOORD1) : COLOR { return …; }
Разберем теперь, как осуществляется преобразование вершины в вершинном шейдере. Как мы уже знаем, трансформация вершины осуществляется путем умножения вектор-строки, описывающей компоненты вершины, на матрицу преобразования. В языке HLSL данный шаг осуществляется с помощью функции mul.
OUT.position = mul( IN.position, WorldViewProj );
Таким образом, каждая вершина трехмерной модели подвергается обработке с помощью данного преобразования, а результат передается дальше по конвейеру. Ниже приведен пример полного текста кода шейдера.
float4x4 WorldViewProj;
struct VS_INPUT { float4 position : POSITION; float4 color0 : COLOR0; ;
struct VS_OUTPUT { float4 position : POSITION; float4 color0 : COLOR0; };
VS_OUTPUT main( VS_INPUT IN ) { VS_OUTPUT OUT; OUT.position = mul( IN.position, WorldViewProj ); OUT.color0 = IN.color0; return OUT; }
Теперь необходимо рассмотреть каким образом происходит установка значений констант в шейдере из программы. Как мы уже видели, при вызове метода компиляции шейдера (D3DXCompileShaderFromFile), в последнюю переменную данной функции помещается ссылка на так называемую таблицу констант. Именно с помощью данного указателя и происходит присваивание значений константам в шейдере. Реализуется это с помощью вызова методов SetXXX интерфейса ID3DXConstantTable, где XXX – "заменяется" на следующие выражения: Bool, Float, Int, Matrix, Vector. Данные методы имеют три параметра: первый – указатель на устройство вывода, второй – наименование константы в шейдере, и третий – устанавливаемое значение. Так, например, установка значения для матрицы преобразования (WorldViewProj) в приведенном выше примере осуществляется следующим образом.
| C++ | D3DXMATRIX matWorld, matView, matProj, tmp; D3DXMatrixPerspectiveFovLH( &matProj, D3DX_PI/4, 1.0f, 1.0f, 100.0f ); D3DXVECTOR3 positionCamera, targetPoint, worldUp; positionCamera = D3DXVECTOR3(2.0f, 2.0f, -2.0f); targetPoint = D3DXVECTOR3(0.0f, 0.0f, 0.0f); worldUp = D3DXVECTOR3(0.0f, 1.0f, 0.0f); D3DXMatrixLookAtLH(&matView, &positionCamera, &targetPoint, &worldUp); D3DXMatrixRotationY(&matWorld, angle); tmp = matWorld * matView * matProj; ConstantTable->SetMatrix( device, "WorldViewProj", &tmp ); |
| Pascal | var matWorld, matView, matProj, tmp: TD3DMatrix; positionCamera, targetPoint, worldUp : TD3DXVector3; ... positionCamera:=D3DXVector3(2,2,-2); targetPoint:=D3DXVector3(0,0,0); worldUp:=D3DXVector3(0,1,0); D3DXMatrixLookAtLH(matView, positionCamera, targetPoint, worldUp); D3DXMatrixPerspectiveFovLH(matProj, PI/4, 1, 1, 100); D3DXMatrixRotationY(matWorld, angle); D3DXMatrixMultiply(tmp, matWorld, matView); D3DXMatrixMultiply(tmp, tmp, matProj); ConstantTable.SetMatrix(device, 'WorldViewProj', tmp); |
Ниже приведены примеры вызова каждого метода.
| C++ | LPD3DXCONSTANTTABLE ConstantTable = NULL; bool b = true; ConstantTable->SetBool( device, "flag", b ); float f = 3.14f; ConstantTable->SetFloat( device, "pi", f ); int x = 4; ConstantTable->SetInt( device, "num", x ); D3DXMATRIX m; ... ConstantTable->SetMatrix( device, "mat", &m ); D3DXVECTOR4 v(1.0f, 2.0f, 3.0f, 4.0f); ConstantTable->SetVector( device, "vec", &v ); |
| Pascal | var b: Boolean; f: Single; x: Integer; m: TD3DMatrix; v: TD3DXVector4; ConstantTable: ID3DXConstantTable; ... b := true; ConstantTable.SetBool(device, 'flag', b); f:=3.14; ConstantTable.SetFloat(device, 'pi', f); x := 4; ConstantTable.SetInt(device, 'num', x); m._11:=1; ... ConstantTable.SetMatrix(device, 'mat', m); v := D3DXVector4(1,2,3,4); ConstantTable.SetVector(device, 'vec', v); |







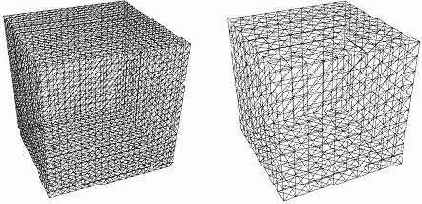
В качестве веса вершины пусть выступает значение координаты y, а матрицы



При этом код вершинного шейдера будет выглядеть следующим образом.
float4x4 M1; float4x4 M2;
struct VS_INPUT { float4 position : POSITION; float4 color0 : COLOR0; };
struct VS_OUTPUT { float4 position : POSITION; float4 color0 : COLOR0; };
VS_OUTPUT main( VS_INPUT IN ) { VS_OUTPUT OUT; float4x4 m = (1-IN.position.y)*M1 + IN.position.y*M2; OUT.position = mul( IN.position, m ); OUT.color0 = IN.position; return OUT; }
Присутствующие в шейдере матрицы преобразования


| C++ | D3DXMATRIX matWorld1, matWorld2, matView, matProj, M1, M2; LPD3DXCONSTANTTABLE ConstantTable = NULL; D3DXMatrixRotationY(&matWorld1, 30.0f*D3DX_PI/4); M1 = matWorld1 * matView * matProj; ConstantTable->SetMatrix( device, "M1", &M1 ); D3DXMatrixRotationY(&matWorld2, -30.0f*D3DX_PI/4); M2 = matWorld2 * matView * matProj; ConstantTable->SetMatrix( device, "M2", &M2 ); |
| Pascal | var matWorld1, matWorld2, matView, matProj, M1, M2: TD3DMatrix; ConstantTable: ID3DXConstantTable; ... D3DXMatrixRotationY(matWorld1, 30*pi/180); D3DXMatrixMultiply(M1, matWorld1, matView); // M1 = matWorld1 * matView D3DXMatrixMultiply(M1, M1, matProj); // M1 = M1 * matProj ConstantTable.SetMatrix(device, 'M1', M1); D3DXMatrixRotationY(matWorld2, - 30*pi/180); D3DXMatrixMultiply(M2, matWorld2, matView); D3DXMatrixMultiply(M2, M2, matProj); ConstantTable.SetMatrix(device, 'M2', M2); |

Рассмотрим теперь необходимые шаги для работы с пиксельным шейдером. В отличие от вершинных шейдеров, пиксельные шейдеры не могут эмулироваться центральным процессором. Поэтому если видеокарта не поддерживает пиксельных шейдеров, значит обработка элементарных фрагментов (пикселей) будет производится по жестко заданному правилу.
Как мы уже говорили, пиксельный шейдер представляет собой небольшую программу (процедуру) для обработки каждого пикселя. Первым шагом необходимо объявить переменную интерфейсного типа IDirect3DPixelShader9, которая отвечает за работу пиксельного шейдера из программы.
| C++ | LPDIRECT3DPIXELSHADER9 PixelShader = NULL; |
| Pascal | var PixelShader: IDirect3DPixelShader9; |
| C++ | LPD3DXBUFFER Code = NULL; LPD3DXBUFFER BufferErrors = NULL; LPD3DXCONSTANTTABLE ConstantTable = NULL; D3DXCompileShaderFromFile( "pixel.psh", NULL, NULL, "main", "ps_1_0", 0, &Code, &BufferErrors, &ConstantTable ); |
| Pascal | var Code: ID3DXBuffer; BufferErrors: ID3DXBuffer; ConstantTable: ID3DXConstantTable; ... D3DXCompileShaderFromFile('pixel.psh', nil, nil, 'Main', 'ps_1_0', 0, @Code, @BufferErrors, @ConstantTable); |
| C++ | LPDIRECT3DPIXELSHADER9 PixelShader = NULL; device->CreatePixelShader( (DWORD*)Code->GetBufferPointer(), &PixelShader ); |
| Pascal | var PixelShader: IDirect3DPixelShader9; ... device.CreatePixelShader(Code.GetBufferPointer, PixelShader); |
| C++ | device->SetPixelShader( PixelShader ); |
| Pascal | device.SetPixelShader(PixelShader); |
struct PS_INPUT { float4 color: COLOR; };
struct PS_OUTPUT { float4 color : COLOR; };
PS_OUTPUT main (PS_INPUT input) { PS_OUTPUT output; output.color = input.color; return output; };
В данном случае пиксельный шейдер фактически просто "проталкивает" пиксель дальше по графическому конвейеру, не подвергая его никакой обработке. Рассмотрим несколько способов возможной обработки точек в пиксельном шейдере на примере плоского цветного треугольника.
| "проталкивание" пикселя | output.color = input.color; |  |
| инвертирование цветов | output.color = 1-input.color; |  |
| увеличение яркости | output.color = 2*input.color; |  |
| уменьшение яркости | output.color = 0.5*input.color; |  |
| блокирование цветового канала | output.color = input.color; output.color.r = 0; |  |
| сложная обработка | output.color.r=0.5*input.color.r; output.color.g=2.0*input.color.g; output.color.b=input.color.b*input.color.b; |  |
sampler tex0;
struct PS_INPUT { float2 base : TEXCOORD0; };
struct PS_OUTPUT { float4 diffuse : COLOR0; };
PS_OUTPUT Main (PS_INPUT input) { PS_OUTPUT output; output.diffuse = tex2D(tex0, input.base); return output; };
В первой строке шейдера объявляется семплер (tex0). Операция выбора текселя из семплера называют семплированием. Следует заметить, что входная структура шейдера (PS_INPUT) содержит лишь текстурные координаты пикселя. Вообще говоря, в пиксельный шейдер можно передавать те данные, которые программист считает нужными (цвет вершины, вектор нормали, положение источника света и т.д.).
Например, ниже приводится пример, в котором входная структура пиксельного шейдера содержит цвет и двое текстурных координат.
struct PS_INPUT { float2 uv0 : TEXCOORD0; float2 uv1 : TEXCOORD1; float4 color : COLOR0; };
Пусть у нас вершина описана через положение на плоскости (преобразованная вершина), цвет и две текстурные координаты:
| C++ | struct MYVERTEX { FLOAT x, y, z, rhw; DWORD color; FLOAT u1, v1; FLOAT u2, v2; } #define MY_FVF (D3DFVF_XYZRHW | D3DFVF_DIFFUSE | D3DFVF_TEX2); |
| Pascal | type MyVertex = packed record x, y, z, rhw: Single; color: DWORD; u1,v1: Single; u2,v2: Single; end; const MY_FVF = D3DFVF_XYZRHW or D3DFVF_DIFFUSE or D3DFVF_TEX2; |
 |  |  |
| Текстура1 | Текстура2 | Закраска квадрата |
sampler tex0; sampler tex1;
struct PS_INPUT { float2 uv0 : TEXCOORD0; float2 uv1 : TEXCOORD1; float4 color: COLOR0; };
struct PS_OUTPUT { float4 diffuse : COLOR0; };
PS_OUTPUT Main (PS_INPUT input) { PS_OUTPUT output; float4 texel0 = tex2D(tex0, input.uv0); float4 texel1 = tex2D(tex1, input.uv1); output.diffuse = ...; return output; };
Некоторые способы взаимодействия двух этих поверхностей (текстуры и цветного квадрата) представлены в таблице.
| output.diffuse = texel0*texel1; |  |
| output.diffuse = texel0*texel1+input.color; |  |
| output.diffuse = texel0+texel1*input.color; |  |
| output.diffuse = texel0*texel1*input.color; |  |
PS_OUTPUT output; const float
|
sampler tex0; struct PS_INPUT { float2 base : TEXCOORD0; }; struct PS_OUTPUT { float4 diffuse : COLOR0; }; PS_OUTPUT Main (PS_INPUT input) { PS_OUTPUT output; const float W =320.0f; const float H =240.0f; const float du=1.0f/(W-1); const float dv=1.0f/(H-1); const float2 c[9] = { float2(-du, -dv), float2(0.0f, -dv), float2(du, -dv), float2(-du, 0.0f), float2(0.0f, 0.0f), float2(du, 0.0f), float2(-du, dv), float2(0.0f, dv), float2(du, dv) }; float3 col[9]; for (int i=0; i<9; i++) { col[i] = tex2D(tex0, input.base+c[i]); } float lum[9]; float3 gray = (0.30f, 0.59f, 0.11f) ; for (int i=0; i<9; i++) { lum[i] = dot(col[i], gray); } float res1 = 0.0f; float res2 = 0.0f; const float sobel1[9] = { 1, 2, 1, 0, 0, 0, -1, -2, -1}; const float sobel2[9] = {-1, 0, 1, -2, 0, 2, -1, 0, 1}; const float tisnenie[9] = {0, 1, 0, -1, 0, 1, 0, -1, 0}; for (int i=0; i<9; i++) { res1+=lum[i]*sobel1[i]; res2+=lum[i]*sobel2[i]; res+=lum[i]*tisnenie[i]; } output.diffuse = sqrt(res1*res1+res2*res2); //output.diffuse = res+0.5f; return output; }; |
| Пример 6.1. |
| Закрыть окно |
sampler tex0;
struct PS_INPUT
{
float2 base : TEXCOORD0;
};
struct PS_OUTPUT
{
float4 diffuse : COLOR0;
};
PS_OUTPUT Main (PS_INPUT input)
{
PS_OUTPUT output;
const float W =320.0f;
const float H =240.0f;
const float du=1.0f/(W-1);
const float dv=1.0f/(H-1);
const float2 c[9] = {
float2(-du, -dv), float2(0.0f, -dv), float2(du, -dv),
float2(-du, 0.0f), float2(0.0f, 0.0f), float2(du, 0.0f),
float2(-du, dv), float2(0.0f, dv), float2(du, dv)
};
float3 col[9];
for (int i=0; i<9; i++) {
col[i] = tex2D(tex0, input.base+c[i]);
}
float lum[9];
float3 gray = (0.30f, 0.59f, 0.11f) ;
for (int i=0; i<9; i++) {
lum[i] = dot(col[i], gray);
}
float res1 = 0.0f;
float res2 = 0.0f;
const float sobel1[9] = { 1, 2, 1, 0, 0, 0, -1, -2, -1};
const float sobel2[9] = {-1, 0, 1, -2, 0, 2, -1, 0, 1};
const float tisnenie[9] = {0, 1, 0, -1, 0, 1, 0, -1, 0};
for (int i=0; i<9; i++) {
res1+=lum[i]*sobel1[i];
res2+=lum[i]*sobel2[i];
res+=lum[i]*tisnenie[i];
}
output.diffuse = sqrt(res1*res1+res2*res2);
//output.diffuse = res+0.5f;
return output;
};
Файлы эффектов
В состав библиотеки Direct3D входит набор средств, которые предоставляют некий оберточный механизм для работы с вершинными и пиксельными шейдерами, установкой текстурных состояний и константами. Данная возможность реализуется с помощью интерфейса ID3DXEffect. Данный "оберточный" интерфейс инкапсулирует в себе следующие особенности:
Содержат глобальные переменные, которые можно устанавливать из приложения;Позволяют манипулировать (управлять) состоянием механизма воспроизведения;Управляют текстурными состояниями и состояниями семплеров (определяют файлы текстур, инициализируют текстурные уровни и их настройки);Управляют механизмом визуализации с помощью шейдеров;
Рассмотрим пример использования файлов эффектов, написанных на языке HLSL. Ниже представлен простейший пример файла эффектов.
float4x4 WorldViewProj; float4x4 World; float4 Light;
texture Tex0 < string name = "texture.bmp"; >;
struct VS_INPUT { float4 position : POSITION; float3 normal : NORMAL; float2 texcoord : TEXCOORD0; };
struct VS_OUTPUT { float4 position : POSITION; float4 color : COLOR0; float2 texcoord : TEXCOORD0; };
VS_OUTPUT main_vs( VS_INPUT In ) { VS_OUTPUT Out; Out.position = mul( In.position, WorldViewProj ); float3 pos = mul( In.position, World ); float3 light = normalize(vecLight-pos); float3 normal = normalize(mul( In.normal, World )); float4 green = {0.0f, 1.0f, 0.0f, 1.0f}; Out.texcoord = In.texcoord; Out.color = green*dot(light, normal); return Out; }
sampler Sampler = sampler_state { Texture = (Tex0); MipFilter = LINEAR; MinFilter = LINEAR; MagFilter = LINEAR; };
struct PS_INPUT { float2 texcoord : TEXCOORD0; float4 color : COLOR0; };
float4 main_ps( PS_INPUT In ) : COLOR0 { return tex2D(Sampler, In.texcoord ) * In.color; }
technique tec0 { pass p0 { VertexShader = compile vs_1_1 main_vs(); PixelShader = compile ps_1_1 main_ps(); } }
Пример 6.2.
Как видно из представленного примера, файлы эффектов объединяют в себе вершинный, пиксельный шейдеры, а также различные настройки режима воспроизведения.
Кроме того, файлы эффектов позволяют объединить ряд вариантов воспроизведения в одном файле. Такая модульность открывает широкие возможности по использованию одной программы на различных аппаратных решениях (компьютерах с различными техническими возможностями). Каждый файл эффектов может содержать один и более разделов technique, которые как раз и предназначены для различных способов реализации алгоритма воспроизведения. Каждый раздел techniques может содержать внутри себя один и более разделов rendering pass, которые объединяют в себе состояния устройства вывода, текстурные уровни, шейдеры. Следует заметить, что файлы эффектов не ограничены в использовании только программируемых элементов графического конвейера (шейдеров). Они также могут использоваться и в фиксированном конвейере для управления состояниями устройства вывода, источниками света, материала ми и текстурами. Применение нескольких разделов rendering pass позволяют получить различные эффекты визуализации, например, двухпроходный алгоритм построения тени с использованием буфера трафарета. Ниже представлен шаблон файла эффектов, в котором присутствует два раздела technique, плюс к этому второй раздел содержит два подраздела rendering pass.
technique tec0 { pass p0 // первый и единственный раздел rendering pass { // состояние устройства вывода, шейдеры, семплеры } }
technique tec1 { pass p0 // первый rendering pass { // состояние устройства вывода, шейдеры, семплеры }
pass p1 // второй раздел rendering pass { // состояние устройства вывода, шейдеры, семплеры } }
Для управления файлами эффектов из приложения необходимо воспользоваться методами интерфейса ID3DXEffect. Вначале необходимо объявить переменную интерфейсного типа ID3DXEffect, и возможно переменную для буфера ошибок.
| C++ | LPD3DXEFFECT Effect = NULL; LPD3DXBUFFER BufferErrors = NULL; |
| Pascal | var Effect: ID3DXEffect; BufferErrors: ID3DXBuffer; |
Ссылка на устройство вывода;Имя файла эффекта;Набор макро определений (может быть пустым); Указатель на интерфейс ID3DXInclude для обработки включений в файле эффекта (может быть пустым);Набор флагов компиляции (может быть нулем);Указатель на интерфейс ID3DXEffectPool для обработки общих параметров в эффекте (может быть пустым);Указатель на полученный результат;Указатель на буфер ошибок.
| C++ | D3DXCreateEffectFromFile( device, "effect.fx", NULL, NULL, 0, NULL, &Effect, &BufferErrors) |
| Pascal | D3DXCreateEffectFromFile(device, ' effect.fx ', nil, nil, 0, nil, Effect, BufferErrors); |
| C++ | Effect->SetTechnique("tec0"); |
| Pascal | Effect.SetTechnique('tec0'); |
| C++ | unsigned int numPasses = 0; Effect->Begin(&numPasses, 0); for(unsigned int pass = 0; pass < numPasses; pass++) { Effect->BeginPass(pass); device->DrawPrimitive(...); Effect->EndPass(); } Effect->End(); |
| Pascal | var numPasses: DWord; pass: DWord; ... Effect._Begin(@numPasses, 0); for pass:=0 to numPasses-1 do begin Effect.BeginPass(pass); Device.DrawPrimitive(...); Effect.EndPass; end; Effect._End; |
SetBool() SetInt() SetMatrix() SetString() SetTexture() SetVector()
Следует отметить еще одно достоинство файлов эффектов. Для работы с ними существует программа EffectEdit, которая поставляет вместе с DirectX SDK. Эта программа позволяет загружать файлы эффектов и осуществлять рендеринг сцены при установленных настройках графического конвейера (шейдеров, текстур, состоянийустройства воспроизведения и др.). Кроме того, утилита EffectEdit может быть использована в качестве отладочного механизма ваших шейдерных программ.
Обработка ошибок
При использовании графической библиотеки Direct3D программисту следует уделять особе внимание обработке ошибок. Для этих целей предусмотрены два специальных макроса, которые проверяют код на наличие или отсутствие ошибок:
FAILED() SUCCEEDED()
Принцип работы этих макросов очень прост и представлен ниже.
if ( FAILED()) // ошибка при выполнении команды ... else // команда завершилась успешно
Для второго макроса принцип действия будет противоположным.
if (SUCCEEDED ()) // команда завершилась успешно ... else // ошибка при выполнении команды
Ниже приведены некоторые примеры обработки ошибок.
| C++ |
LPDIRECT3D9 direct3d = NULL; ... if( FAILED( direct3d -> CreateDevice( … ) ) ) { // обработка ошибки } |
| Pascal |
var direct3d: IDirect3D9; ... if Failed ( direct3d.CreateDevice( … ) ) then begin // обработка ошибки end; |
Можно осуществлять анализ ошибок через дополнительную переменную.
| C++ |
HRESULT hr; hr = direct3d -> CreateDevice( … ); if( FAILED(hr) ) { } |
| Pascal |
var hr: HRESULT; … hr := direct3d.CreateDevice( … ); if Failed(hr) then begin end |
И еще один способ обработки ошибок заключается в сравнении результата вызова функции с константой D3D_OK.
| C++ |
if ( direct3d -> CreateDevice( … ) != D3D_OK ) { } |
| Pascal |
if direct3d.CreateDevice( … ) <> D3D_OK then begin end; |
Следует также остановиться на обработке ошибок при компиляции шейдеров. Как мы помним, в одном из параметров функции D3DXCompileShaderFromFile(…) возвращается указатель на буфер ошибок. Ниже приводится программный код, позволяющий вывести на экран сообщение об ошибке, полученное от компилятора HLSL.
| C++ |
if ( D3DXCompileShaderFromFile( "shader.psh", NULL, NULL, "main", "ps_2_0", 0, &Code, &BufferErrors, NULL) != D3D_OK ) { MessageBox(NULL, (const char*)BufferErrors->GetBufferPointer(), "Ошибка в шейдере!!!", MB_OK | MB_ICONEXCLAMATION); } |
| Pascal |
if D3DXCompileShaderFromFile('shader.psh', nil, nil, 'Main','ps_2_0', 0, @Code, @BufferErrors, nil) D3D_OK then begin MessageBox(0, BufferErrors.GetBufferPointer, 'Ошибка в шейдере!!!', MB_OK or MB_ICONEXCLAMATION); end; |
Такой информативный способ позволяет легко "увидеть" в какой именно строке шейдера допущена ошибка.
Подсчет количества кадров в секунду
Как правило, показателем производительности в приложениях, связанных с трехмерной графикой, является количество кадров, выводимых приложением в единицу времени (в секунду). Поэтому очень часто возникает необходимость вычислить и отобразить эту информацию в окне приложения. Ниже приведен пример, показывающий как подсчитывать количество кадров в секунду.
| C++ |
count = 0; last_tick = GetTickCount(); while(msg.message != WM_QUIT) { if(PeekMessage(&msg, 0, 0, 0, PM_REMOVE)) { TranslateMessage(Msg); DispatchMessage(Msg); } else { this_tick = GetTickCount(); if(this_tick-last_tick>=1000) { last_tick=this_tick; fps=count; count=0; // вывод значения fps } else count++ Render(); } } |
| Pascal |
count:=0; last_tick:=GetTickCount(); while Msg.message <> WM_QUIT do begin if PeekMessage(msg, 0, 0, 0, PM_REMOVE) then begin TranslateMessage(Msg); DispatchMessage(Msg); end else begin this_tick:=GetTickCount(); if(this_tick-last_tick>=500) then begin last_tick:=this_tick; fps:=count; count:=0; // вывод значения fps end else count:=count+1; Render; end; end; |

Полноэкранный режим воспроизведения
До сих пор вывод всех сцен построения производился в окно (на форму). Библиотека Direct3D позволяет осуществить рендеринг в полноэкранном режиме (Full Screen). Для перехода в полноэкранный режим вывода примитивов необходимо лишь при заполнении структуры D3DPRESENT_PARAMETERS явно указать размеры заднего буфера (BackBuffer), установить флаг Windowed в значение FALSE. Также нужно указать режим переключения первичного и вторичного (заднего) буферов рендеринга и определить интервал смены буферов.
| C++ |
D3DPRESENT_PARAMETERS params; … ZeroMemory( ¶ms, sizeof(params) ); params.Windowed = FALSE; params.SwapEffect = D3DSWAPEFFECT_FLIP; params.BackBufferWidth = 1280; params.BackBufferHeight = 1024; params.BackBufferFormat = display.Format; params.PresentationInterval = D3DPRESENT_INTERVAL_IMMEDIATE; … |
| Pascal |
var params: TD3DPresentParameters; … ZeroMemory( @params, SizeOf(params) ); params.Windowed := False; params.SwapEffect := D3DSWAPEFFECT_FLIP; params.BackBufferWidth := 1280; params.BackBufferHeight := 1024; params.BackBufferFormat := display.Format; params.PresentationInterval := D3DPRESENT_INTERVAL_IMMEDIATE; … |
Единственно, что необходимо еще проделать – это организовать возможность выхода (закрытия) программы. Для этого можно, например, обработать событие системы WM_KEYDOWN. Полноэкранный режим довольно часто используют в играх, так как именно при таком режиме достигается максимальная производительность видеокарты. Можно воспользоваться функцией Win32 API GetSystemMetrics() для того, чтобы узнать текущее разрешение экрана.
| C++ |
D3DPRESENT_PARAMETERS params; … params.BackBufferWidth = GetSystemMetrics(SM_CXSCREEN); params.BackBufferHeight = GetSystemMetrics(SM_CYSCREEN); |
| Pascal |
var params: TD3DPresentParameters; … params.BackBufferWidth := GetSystemMetrics(SM_CXSCREEN); params.BackBufferHeight := GetSystemMetrics(SM_CYSCREEN); |
float4x4 WorldViewProj; float4x4 World; float4
|
float4x4 WorldViewProj; float4x4 World; float4 Light; texture Tex0 < string name = "texture.bmp"; >; struct VS_INPUT { float4 position : POSITION; float3 normal : NORMAL; float2 texcoord : TEXCOORD0; }; struct VS_OUTPUT { float4 position : POSITION; float4 color : COLOR0; float2 texcoord : TEXCOORD0; }; VS_OUTPUT main_vs( VS_INPUT In ) { VS_OUTPUT Out; Out.position = mul( In.position, WorldViewProj ); float3 pos = mul( In.position, World ); float3 light = normalize(vecLight-pos); float3 normal = normalize(mul( In.normal, World )); float4 green = {0.0f, 1.0f, 0.0f, 1.0f}; Out.texcoord = In.texcoord; Out.color = green*dot(light, normal); return Out; } sampler Sampler = sampler_state { Texture = (Tex0); MipFilter = LINEAR; MinFilter = LINEAR; MagFilter = LINEAR; }; struct PS_INPUT { float2 texcoord : TEXCOORD0; float4 color : COLOR0; }; float4 main_ps( PS_INPUT In ) : COLOR0 { return tex2D(Sampler, In.texcoord ) * In.color; } technique tec0 { pass p0 { VertexShader = compile vs_1_1 main_vs(); PixelShader = compile ps_1_1 main_ps(); } } |
| Пример 6.2. |
| Закрыть окно |
float4x4 WorldViewProj;
float4x4 World;
float4 Light;
texture Tex0 < string name = "texture.bmp"; >;
struct VS_INPUT
{
float4 position : POSITION;
float3 normal : NORMAL;
float2 texcoord : TEXCOORD0;
};
struct VS_OUTPUT
{
float4 position : POSITION;
float4 color : COLOR0;
float2 texcoord : TEXCOORD0;
};
VS_OUTPUT main_vs( VS_INPUT In )
{
VS_OUTPUT Out;
Out.position = mul( In.position, WorldViewProj );
float3 pos = mul( In.position, World );
float3 light = normalize(vecLight-pos);
float3 normal = normalize(mul( In.normal, World ));
float4 green = {0.0f, 1.0f, 0.0f, 1.0f};
Out.texcoord = In.texcoord;
Out.color = green*dot(light, normal);
return Out;
}
sampler Sampler = sampler_state
{
Texture = (Tex0);
MipFilter = LINEAR;
MinFilter = LINEAR;
MagFilter = LINEAR;
};
struct PS_INPUT
{
float2 texcoord : TEXCOORD0;
float4 color : COLOR0;
};
float4 main_ps( PS_INPUT In ) : COLOR0
{
return tex2D(Sampler, In.texcoord ) * In.color;
}
technique tec0
{
pass p0
{
VertexShader = compile vs_1_1 main_vs();
PixelShader = compile ps_1_1 main_ps();
}
}
Расчет освещенности с помощью шейдеров
Рассмотрим теперь более подробно, как осуществляется расчет освещенности грани в библиотеке Direct3D. При закраске поверхностей объекта в идеале мы должны для каждой точки грани (полигона) вычислять интенсивность освещения методами, описанными выше. Во многих графических библиотеках, в том числе и в Direct3D прибегают к приближенным методам закраски граней трехмерного объекта, состоящего из полигонов в силу того, что процесс вычисления значения интенсивности для каждого пикселя, является вычислительно трудоемким. В компьютерной графике используют, как правило, три основных способа закраски полигональной сетки: однотонная закраска, закраска, основанная на интерполяции значений интенсивности, и закраска, построенная на основе интерполяции векторов нормали. Библиотека Direct3D располагает способами использования только двух первых методов.
При однотонной закраске вычисляется один уровень интенсивности, который используется для закраски всего полигона. При использовании закраски этого типа будет проявляться эффект резкого перепада интенсивности на всех граничных ребрах объекта.
Метод закраски, который основан на интерполяции интенсивности (метод Гуро), позволяет устранить дискретность изменения интенсивности. Процесс закраски по методу Гуро осуществляется следующими шагами:
определяется (вычисляется или изначально задается) нормаль к каждой вершине полигона; причем для различных полигонов, имеющих общую вершину, нормали, как правило, различаются;вычисляются значения интенсивности в каждой вершине полигона, используя рассмотренные выше модели освещенности;полигон закрашивается путем линейной интерполяции значений интенсивностей в вершинах сначала вдоль каждого ребра, а затем и между ребрами вдоль каждой сканирующей строки
В некоторых экзотических случаях и метод закраски Гуро не позволяет полностью устранить перепады интенсивности. В этом случае можно воспользоваться закраской по методу Фонга. Алгоритмически метод Фонга схож с методом Гуро. Но в отличие от интерполяции значений интенсивности в методе Гуро, в методе Фонга используется интерполяция векторов нормали вдоль сканирующей строки.
Функция mul() производит умножение вектора на матрицу, функция normalize() осуществляет нормировку вектора, функция dot() вычисляет скалярное произведение двух векторов. Как видно из представленных строк кода, для каждой вершины мы должны определять вектор на источник света и преобразовывать нормаль, как показано ниже.
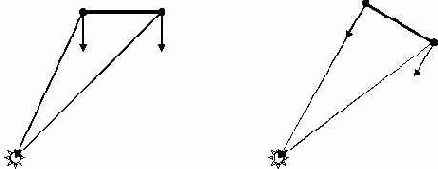
Таким образом, каждая вершина трехмерной модели получит цвет в соответствие с ее нормалью и вектором на источник. После выполнения этих шагов все вершины передаются на этап компоновки примитивов и растеризации. Растеризатор делит каждый треугольник на элементарные фрагменты (пиксели) и затем производит линейную интерполяцию текстурных координат и цвета.
Такой способ обработки дает возможность реализовать попиксельное освещение граней объекта. Реализовать это можно следующим образом. В силу того, что все атрибуты вершины (положение, цвет, текстурные координаты и т.д.), вычисленные в вершинном шейдере, интерполируются "по треугольнику", то можно, например, в качестве текстурных координат передать значения нормали вершины. Таким образом, графический конвейер воспримет нормаль как текстурные координаты вершины, и для каждого растеризуемого пикселя произведет интерполяцию векторов нормали. Входными данными для вершинного шейдера будут координаты вершины и нормаль.
struct VS_INPUT { float4 position : POSITION; float3 normal : NORMAL; };
Выходные данные вершинного шейдера мы описываем уже тройкой атрибутов: преобразованная вершина, преобразованная нормаль и вектор на источник света.
struct VS_OUTPUT { float4 position : POSITION; float3 light : TEXCOORD0; float3 normal : TEXCOORD1; };
Следует заметить, что атрибуты вершины нормаль и вектор на источник определены как текстурные координаты размерности 3 (float3). Тело вершинного шейдера будет выглядеть следующим образом.
VS_OUTPUT main_vs( VS_INPUT In ) { VS_OUTPUT Out; Out.position = mul( In.position, WorldViewProj ); float3 pos = mul( In.position, World ); Out.light = normalize(vecLight-pos); Out.normal = normalize(mul( In.normal, World )); return Out; }
Глобальные переменные будут такими же как и в предыдущем случае.
float4x4 WorldViewProj; float4x4 World; float4 vecLight;
Таким образом, пиксельный шейдер будет приминать на вход всего два вершинных атрибута: нормаль и вектор на источник. Сама же процедура пиксельного шейдера будет выглядеть так.
float4 main_ps(float3 light : TEXCOORD0, float3 normal : TEXCOORD1) : COLOR0 { float4 diffuse = {1.0f, 1.0f, 0.0f, 1.0f}; return diffuse*dot(light, normal); }
Ниже приведены примеры закраски по методу Гуро (слева) и Фонга (справа).
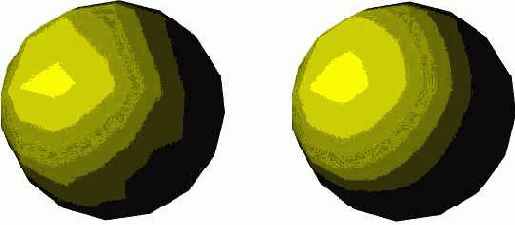
Рассмотрим еще один очень распространенный эффект построения реалистичных изображений, называемый bump-mapping или микрорельефное текстурирование, причем без существенных вычислительных затрат. Идея этого подхода заключается в моделировании рельефной поверхности с помощью двух текстур. Одна из них представляет собой изображение некоторой поверхности, а другая – так называемая карта нормалей. Карта нормалей представляет собой текстуру, где каждый пиксель является вектором нормали. Можно сказать, что карта нормалей несет в себе информацию о неровностях в каждом пикселе изображения. Как известно интенсивность освещения зависит от угла между нормалью в точке и вектором на источник света (закон косинусов Ламберта).
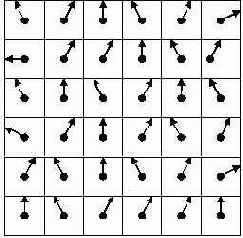
В зависимости от вектора нормали интенсивность в каждом пикселе будет различной. Следует заметить, что вектор нормали (nx, ny, nz) и цвет (R, G, B) кодируется тройкой чисел. Но цвет кодируется тремя положительными величинами из отрезка [0, 1], тогда как компоненты вектора нормали могут принимать и отрицательные значения. Так как координаты нормализованного вектора лежат в диапазоне [-1, 1], то можно с помощью линейного преобразования отобразить отрезок [-1, 1] в отрезок [0, 1]. Для этого можно воспользоваться следующей формулой: N*0.5+0.5, где N –вектор нормали. Такой процесс кодировки проделывается для каждого компонента вектора. Обратное преобразование (отрезок [0, 1] отобразить в отрезок [-1, 1]) может быть реализовано с помощью формулы 2*C–1, где C – значение цвета.
Например, вектор (1, 0, 1) будет преобразован в тройку чисел (1, 0.5, 1) – светло- фиолетовый цвет. Для получения карты нормалей из исходного изображения имеются специальные программы и алгоритмы, например, существует плагин к PhotoShop’у, с помощью которого можно получить карту нормалей. Ниже представлен пример текстуры и соответствующая ей карта нормалей.
 |  |
| Исходное изображение | Карта нормалей |
Получить цвет из исходной текстуры;Получить закодированное значение вектора нормали из карты нормалей;Произвести преобразование значений из цветового пространства в пространство нормалей;Вычислить скалярное произведение нормали на вектор источника света;Умножить полученное значение на цвет исходной текстуры.
Пиксельный шейдер, реализующий данные шаги показан ниже.
float4 Light; sampler tex0; sampler tex1;
struct PS_INPUT { float2 uv0 : TEXCOORD0; float2 uv1 : TEXCOORD1; float4 color: COLOR0; };
float4 Main (PS_INPUT input): COLOR0 { float4 texel0 = tex2D(tex0, input.uv0); float4 texel1 = 2.0f*tex2D(tex1, input.uv1) - 1.0f; return texel0*dot(normalize(Light), texel1); };
Значение положения источника света передается в пиксельный шейдер через переменную Light. Ниже показаны примеры микротекстурирования при различных положениях источника света.
 |  |
| return texel0*dot(normalize(Light), texel1); | |
 |  |
| return input.color*texel0*dot(normalize(Light), texel1); | |
Дополнительные материалы
Ниже приводятся типовые варианты лабораторных работ.
Лабораторная работа № 1
Разработать программу, обеспечивающую вывод на форму большого числа (более 10000) плоских геометрических примитивов (точек, отрезков, треугольников) с использованием библиотеки Direct3D и определить количество выводимых кадров в секунду для каждого типа примитивов. Выходные данные программы (результаты) оформить в виде таблицы следующего вида:
| Несвязные отрезки | 10000 | 40 |
| … | … | … |
Лабораторная работа № 2
Разработать программу, обеспечивающую визуализацию прямоугольников произвольного размера с наложенной текстурой и их вращение вокруг собственного центра масс. Размеры прямоугольников и текстур должны быть степенью двойки. Результаты оформить в виде таблицы:
| 2000 | 512х512 | 25 |
| … | … | … |
Лабораторная работа № 3
Разработать программу, реализующую вращение текстурированного выпуклого полупрозрачного объекта. В качестве результата вывести количество кадров в секунду.
Лабораторная работа № 4
Разработать программу, обеспечивающую визуализацию трехмерного объекта произвольной сложности, освещенного точечными источниками, и отбрасывающего тень на плоскость y=0. Результаты оформить в виде таблицы:
| 3000 | 3 | 20 |
| … | … | … |
Лабораторная работа № 5
Разработать программу, реализующую преобразование трехмерного объекта при помощи эффекта скручивания (blending vertex). Вершинный шейдер должен быть написан на языке HLSL. В качестве результата вывести количество кадров в секунду.
Лабораторная работа № 6
Разработать программу, обеспечивающую попиксельную закраску трехмерного объекта методами Гуро и Фонга. Пиксельный шейдер должен быть написан на языке HLSL. В качестве результата вывести количество кадров в секунду.
Лабораторная работа № 7
Разработать программу с использованием пиксельного шейдера, обеспечивающую обработку изображений точечными и пространственными процессами.
Пиксельные шейдеры должны быть написаны на языке HLSL. Результат оформить в виде таблицы.
| 512х512 | фильтр Собеля | 20 |
| … | … | … |
Разработать программу обработки изображений точечными и пространственными процессами с использованием центрального процессора (CPU). Результат оформить в виде таблицы
| 512х512 | фильтр Собеля | 1000 |
| … | … | … |
